Предмет: Алгебра,
автор: dsafk
Решите, пожалуйста, 35 баллов
Приложения:
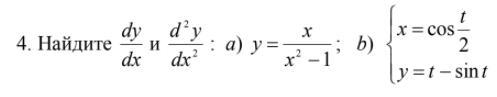
Ответы
Автор ответа:
0
Ответ:
а)
б)
Похожие вопросы
Предмет: Алгебра,
автор: princessdiana2
Предмет: Русский язык,
автор: kattteeeeakir
Предмет: Русский язык,
автор: АлинкаМаслова
Предмет: Алгебра,
автор: Яниска
Предмет: Математика,
автор: Mariamarti