Question

ПОМОГИТЕ ПОЖАЛУЙСТА, СРОЧНО НАДО!!!! 35 БАЛЛОВ.

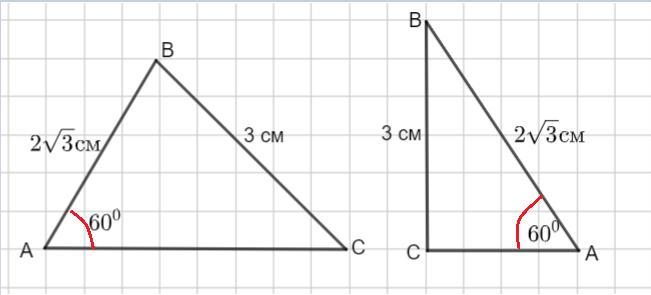
В треугольнике ABC угол A равен 60 градусов, BC = 3 см, AB = 2√3 см. Решите треугольник используя теорему синусов.

Answer 1

Ответ:

∠ С=90°,∠В=30°, АС=√3 см.

Пошаговое объяснение:

По условию дан треугольник АВС.

∠А=60°, ВС= 3 см, АВ=2√3 см.

По теореме синусов: стороны треугольника пропорциональны синусам противолежащих углов.

$\dfrac{AB}{sinC} =\dfrac{BC}{sinA} ;\\\\sinC=\dfrac{AB\cdot sinA}{BC} ;\\\\sinC=\dfrac{2\sqrt{3} \cdot sin60^{0} }{3}=\dfrac{2\sqrt{3} \cdot \dfrac{\sqrt{3} }{2} }{3} =\dfrac{3}{3}=1 ;$

Тогда ∠ С=90° и треугольник АВС - прямоугольный.

Так как сумма острых углов прямоугольного треугольника равна 90°, то ∠В= 90°-60°=30°.

Тогда найдем катет АС , как катет, лежащий напротив угла в 30°.

По свойству: в прямоугольном треугольнике катет, лежащий напротив угла в 30°, равен половине гипотенузы.

$AC=\dfrac{1}{2} AB;\\AC=\dfrac{1}{2}\cdot 2\sqrt{3} =\sqrt{3} ;$

Значит, АС=√3 см.