Question

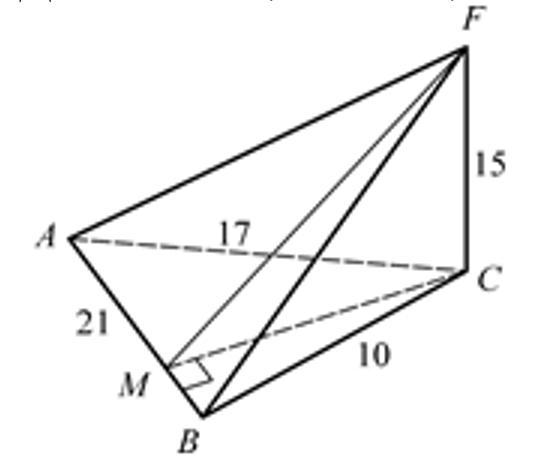
Найдите расстояние от точки F до прямой AB. Дано: ∆ABC, AB = 21, AC = 17, CB = 10, CF (ABC), CF = 15.

Answer 1

Ответ:

17

Объяснение:

СМ⊥АВ, СМ - проекция FM на плоскость (АВС), значит

FM⊥АВ по теореме о трех перпендикулярах.

FM - искомое расстояние.

Полупериметр треугольника АВС:

$p=\dfrac{21+17+10}{2}=\dfrac{48}{2}=24$

Площадь ΔАВС по формуле Герона:

$S=\sqrt{p(p-AB)(p-AC)(p-BC)}$

$S=\sqrt{24\cdot (24-21)\cdot (24-17)\cdot (24-10)}=$

$=\sqrt{24\cdot 3\cdot 7\cdot 14}=$

$=\sqrt{3\cdot 2\cdot 4\cdot 3\cdot 7\cdot 2\cdot 7}=$

$=3\cdot 2\cdot 2\cdot 7=84$

Площадь ΔАВС через высоту:

$S=\dfrac{1}{2}AB\cdot CM$

$CM=\dfrac{2S}{AB}=\dfrac{2\cdot 84}{21}=\dfrac{2\cdot 4\cdot 21}{21}=8$

Из прямоугольного треугольника FCM по теореме Пифагора:

$FM=\sqrt{FC^2+CM^2}=\sqrt{15^2+8^2}=$

$=\sqrt{225+64}=\sqrt{289}=17$