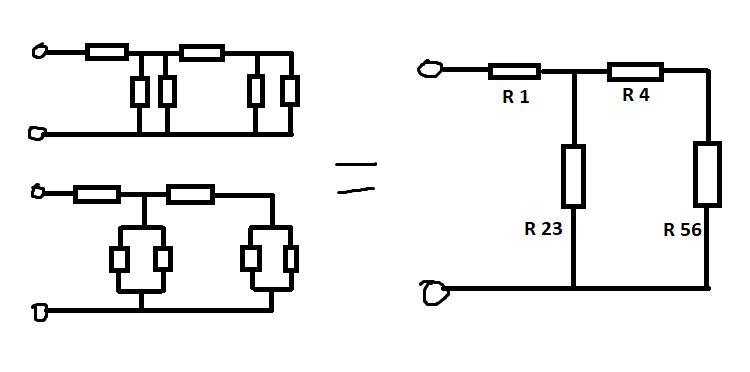
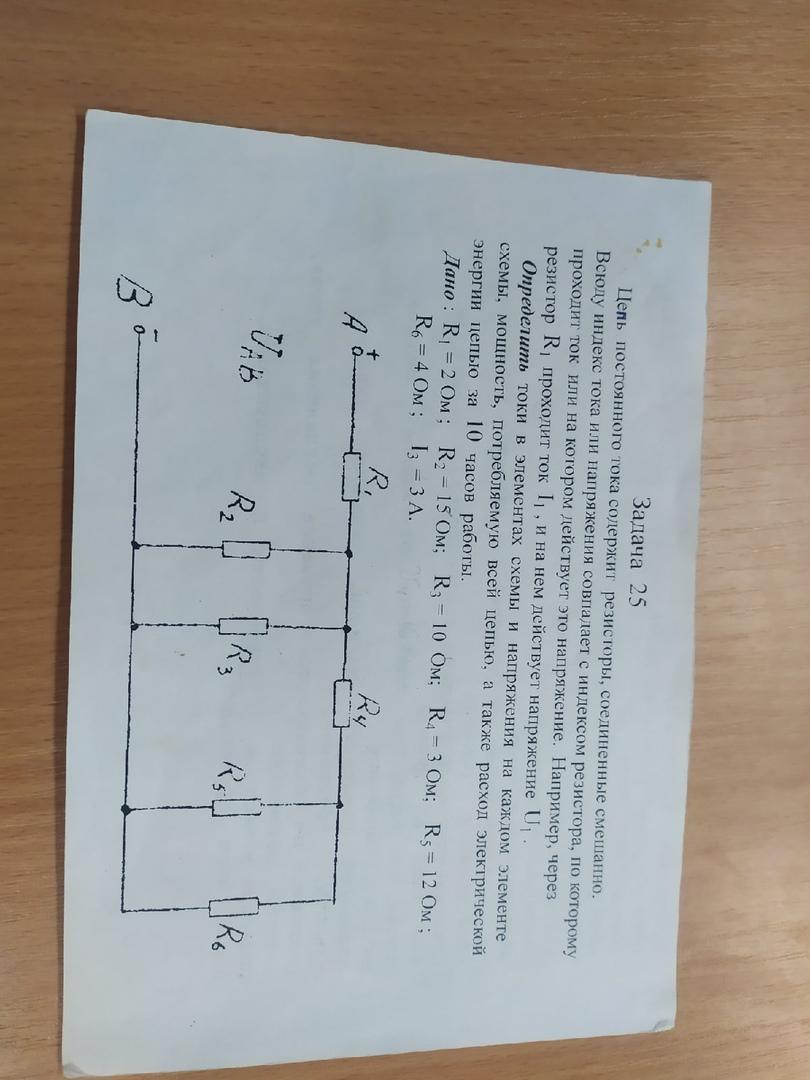
Цепь постоянного тока содержит резисторы, соединенные смешанно. Всюду индекс тока или напряжения совпадает с индексом резистора, по которому проходит ток или на котором действует это напряжение. Например, через резистор R1 Проходит ток I1. и на нем действует напряжение U1.
Определить: Токи в элементах схемы и напряжения на каждом элементе схемы, мощность, потребляемую всей цепью, а также расход электро энергии
цепью за 10 часов.
Ответы
Дано:
R1 = 2 Ом
R2 = 15 Ом
R3 = 10 Ом
R4 = 3 Ом
R5 = 12 Ом
R6 = 4 Ом
I3 = 3 А
t = 10 ч
Найти:
I1, 2, 3, 4, 5, 6 = ?
U1, 2, 3, 4, 5, 6 = ?
P = ?
A (10 ч) = ?
Решение:
Начнём с того, что сила тока I3 позволяет вычислить напряжение U3 и U2, т.е. U3 = U2, т.к. соединение на данном участке цепи параллельное:
U3 = U2 = I3*R3 = 3*10 = 30 В
И тут же сразу можно высчитать силу тока I2:
I2 = U2/R2 = 30/15 = 2 A
I23 = 2 + 3 = 5 A (силы тока cкладываются, потому что соединение параллельное)
Далее лучше преобразовать схему в удобный вид (см. рисунок). Мы можем сообразить, что напряжение U23, которое на концах резистора R23, складывается из напряжений U4 и U56, которые, на концах R4 и R56 соответственно. Т.е.:
U456 = U4 + U56 = U23 - последовательное соединение
То есть, на этом участке можно высчитать силу тока I456, которая будет одинакова как для участка, где расположен резистор R4, так и для участка с эквивалентным резистором R56. Но для начала посчитаем эквивалентный резистор всего участка, то есть надо сложить R4 и R56, предварительно сложив R5 и R6:
R56 = параллельное соединение = 1/(1/R5 + 1/R6) = R5*R6/(R5 + R6) = 12*4/(12 + 4) = 48/16 = 3 Ом
R456 = R4 + R56 = последовательное соединение = 3 + 3 = 6 Ом
Высчитаем силу тока I456:
I456 = U456/R456 = U23/R456 = 30/6 = 5 А
Теперь можно высчитать напряжение для каждого резистора на этом участке:
U4 = I456*R4 = 5*3 = 15 В
U5 = U6 = U56 = I456*R56 = 5*3 = 15 В
Высчитаем силу тока I4, I5 и I6:
I4 = I456 = 5 А
I5 = U5/R5 = 15/12 = 1,25 A
I6 = U6/R6 = 15/4 = 3,75 A
Так, нам известны I2, 3, 4, 5, 6 и U2, 3, 4, 5, 6. Остаётся найти I1 и U1. Анализируем цепь (cм. рисунок). Если участок с резисторами R23, R4 и R56 превратить в участок с одним эквивалентным резистором, то можно понять, что резистор R1 будет соединён с этим эквивалентным последовательно. То есть, напряжение U на концах всей схемы будет складываться из напряжения U1 и U23:
U = U1 + U23
Но нам неизвестно общее напряжение. Зато мы можем найти силу тока на участке с эквивалентным резистором (R23 + R456), которая будет точно такой же на участке с R1 (поскольку соединение R1 с эквивалентным (R23 + R456) является последовательным). Однако, чтобы не усложнять жизнь расчётами, вспомним, что R2 и R3 соединены параллельно. Сила тока на участке с эквивалентным R23 = I2 + I3 = 5 A. Точно так же и R5 c R6: I5 + I6 = 5 A. Эквивалентный R56 соединён с R4 последовательно - сила тока не суммируется. А вот эквивалентный R456 соединён с R23 параллельно, поэтому сила тока будет складываться:
I(23 + 456) = I23 + I456 = 5 + 5 = 10 А
Такая же сила тока, как уже было сказано выше, будет и на участке с R1:
I1 = 10 A
Теперь можно найти напряжение U1:
U1 = R1*I1 = 2*10 = 20 В
Итак:
I1 = 10 A
I2 = 2 A
I3 = 3 A
I4 = 5 A
I5 = 1,75 A
I6 = 3,75 A
U1 = 20 В
U2 = U3 = 30 В
U4 = U5 = U6 = 15 В
Теперь найдём мощность, потребляемую всей цепью:
P = U*I
Общее напряжение будет складываться из U1 и U2, а сила тока всей цепи равна I1, тогда:
P = U*I = (U1 +U2)*I1 = (20 + 30)*10 = 50*10 = 500 Вт
Расход электроэнергии - это работа электрического тока:
A = U*I*t = P*t = 500*10 = 5000 Вт·ч = 5 кВ·ч