Срочно! Решите пожалуйста 2 задание с подробным решением

Ответы
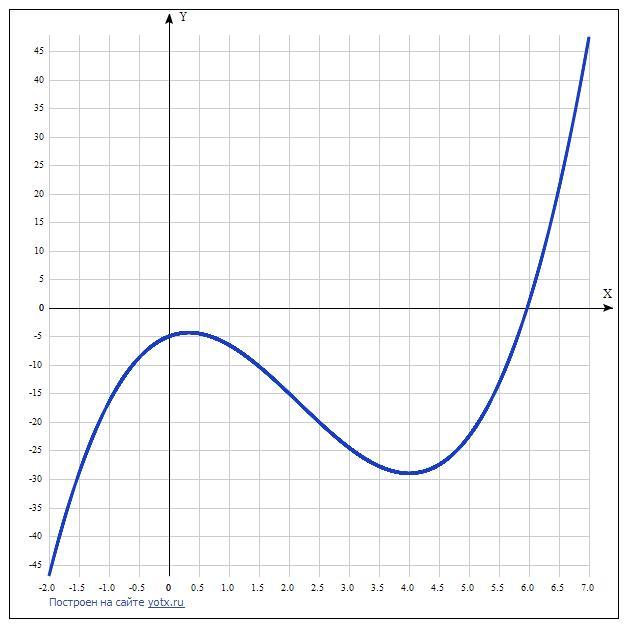
Дано уравнение y = x³ - (13/2)x² + 4x - 5.
1. Экстремумы функции:
Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции:
y' = (x^3-(13/2)x^2+4x-5)' = 3x² -13x+4 = 0.
Решаем это уравнение 3x^2-13x+4=0 и его корни будут экстремумами:
Ищем дискриминант: D=13^2-4*3*4 = 169 - 48 = 121;
Дискриминант больше 0, уравнение имеет 2 корня:
x1=(13 - √121)/(2*3 )= (13-11)/(6) = 1/3;
x2=(13 + √121)/(2*3)=(13+11)/(6)=24/6 = 4.
х1 = 1/3, х2 = 4.
Результат: y’=0. Точки: ((1/3); -4,351852) и (4; -29).
2. Интервалы возрастания и убывания функции:
Имеем 3 интервала монотонности функции: (-∞; (1/3)), ((1/3); 4) и (4; ∞).
На промежутках находим знаки производной. Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = 0 0,3333 1 4 5
y' = 4 0 -6 0 14.
Минимум функции в точке: х = 4,
Максимум функции в точке: х = 1/3.
Возрастает на промежутках: (-∞; (1/3)) и (4; ∞).
Убывает на промежутке: ((1/3); 4).
Так как минимум и максимум функции только локальные, то область значений функции - вся числовая ось: E(y) = R.