Предмет: Геометрия,
автор: lerusiche
Докажите, что если в треугольнике два угла равны, то биссектрисы, проведенные из вершин этих углов, также равны.
Ответы
Автор ответа:
0
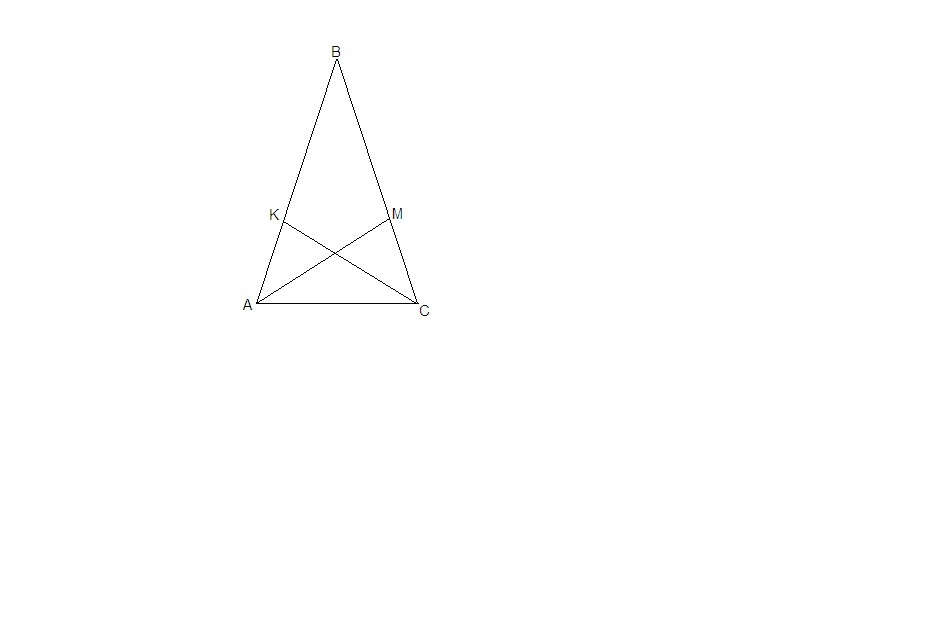
Пусть в треугольнике АВС равны углы ВАС и ВСА. АМ и СК - биссектрисы равных углов.
∠ВАС = ∠ВСА по условию,
∠КСА = ∠МАС как половины равных углов,
АС - общая сторона для треугольников КСА и МАС , ⇒
ΔКСА = ΔМАС по стороне и двум прилежащим к ней углам,
а значит АМ = СК.
∠ВАС = ∠ВСА по условию,
∠КСА = ∠МАС как половины равных углов,
АС - общая сторона для треугольников КСА и МАС , ⇒
ΔКСА = ΔМАС по стороне и двум прилежащим к ней углам,
а значит АМ = СК.
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: Аноним
Предмет: Английский язык,
автор: hdjsjskssksksll
Предмет: История,
автор: Аноним
Предмет: Химия,
автор: pendolf