Question

Даю 80 балов с обьяснением!!! За приколы буду блочить
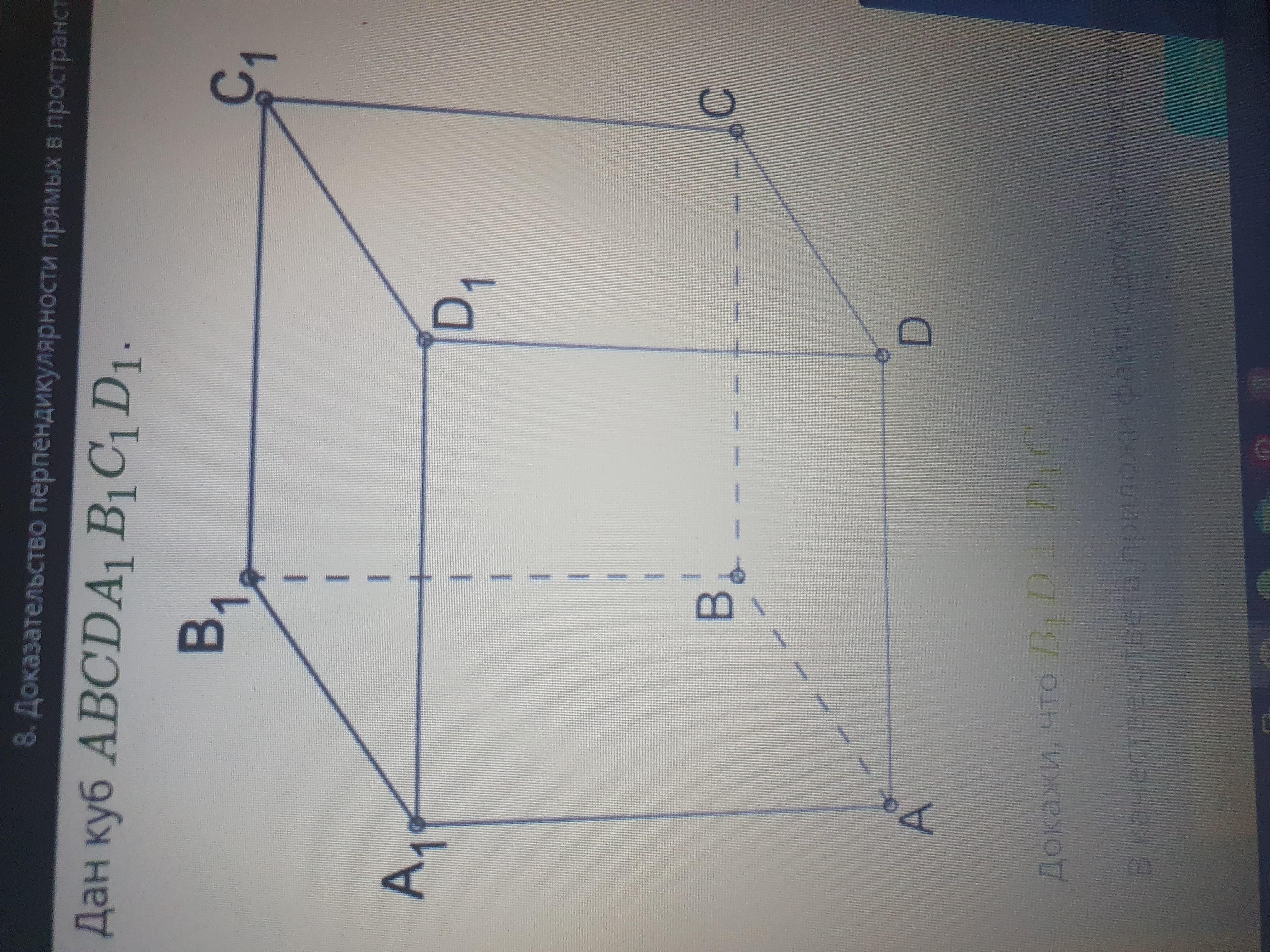
Дан куб ABCDA1B1C1D1
Докажи что B1D перпендикулярен D1C.

Answer 1

Дан куб АВСDА1В1С1D1. Докажите В1D перпендикулярен D1С.

Объяснение:

Введем прямоугольную систему координат: В(0;0;0) ,ось ох по ребру ВА, ось оу по ребру ВС, ось оz по ребру ВВ1 .

Пусть ребро куба а, тогда координаты

В1(0;0;а) ,D (a; a;0) , вектор В1D(a; a;-a) .

D1(a; a; a) ,C(0;a;0), вектор D1C(-a; 0;-a ).

Найдем скалярное произведение в координатах :

В1D×D1C=a×(-a)+a×0+(-a)×(-a)=-a²+0+a²=0. Т.к. скалярное произведение равно нулю, то вектора перпендикулярны, а значит и прямые , на которых лежат эти вектора, перпендикулярны.