Предмет: Геометрия,
автор: aedoaero
Стороны треугольника равны 6 см, 9 см, 13 см. Две стороны другого треугольника-3 см и 4,5 см. Какой длины должна быть третья сторона треугольника, чтобы эти треугольники считались подобными?
Начертить, решить написать дано
Ответы
Автор ответа:
3
Ответ:
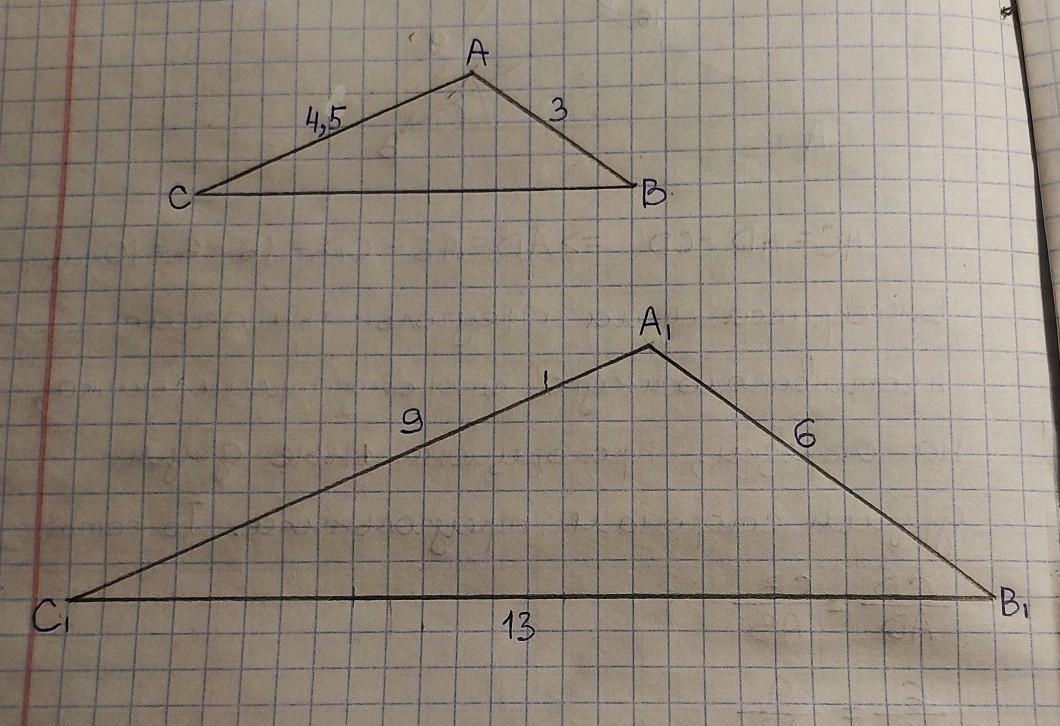
Пусть в ∆А1В1С1: А1В1=6 см, А1С1=9 см, В1С1=13 см. В ∆АВС соответственно: АВ=3 см, АС=4,5 см.
Стороны одного из подобных треугольников пропорциональны сторонам другому, подобного ему, треугольника.
То есть:
Ответ: 6,5 см.
Других вариантов быть не может.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Дашуня03
Предмет: Химия,
автор: sgbm
Предмет: Химия,
автор: khasanibnalali
Предмет: Математика,
автор: бджілка2