Предмет: Математика,
автор: ami579
Найти производные первого порядка для заданных функций.
Приложения:
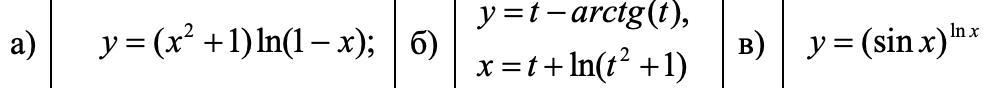
Ответы
Автор ответа:
0
Ответ:
а)
б)
формула:
3)
формула:
Похожие вопросы
Предмет: Русский язык,
автор: Kiesza
Предмет: Математика,
автор: Арианна2004
Предмет: Математика,
автор: Anna20069
Предмет: Математика,
автор: Марго080820050708200
Предмет: Математика,
автор: moma88