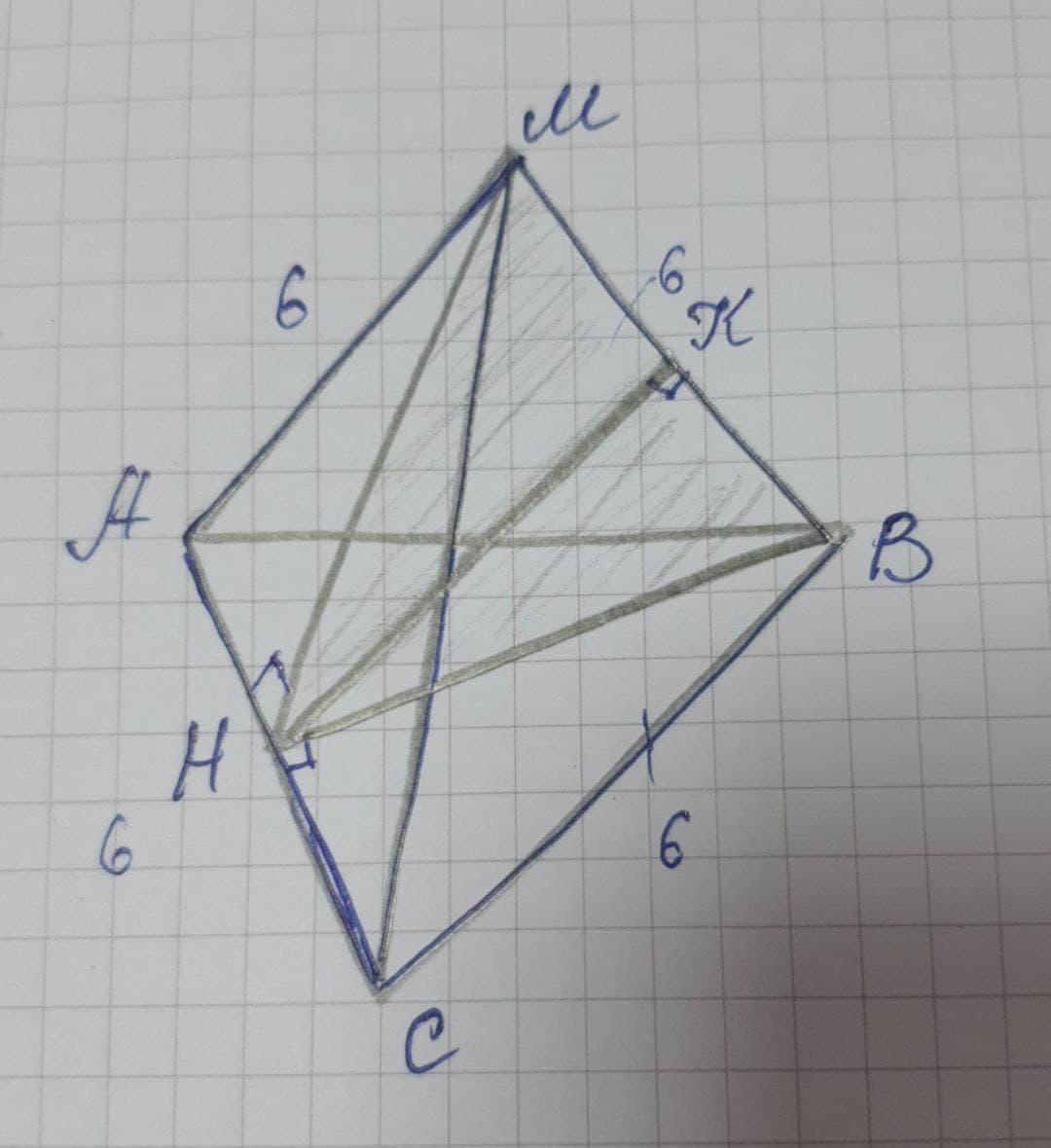
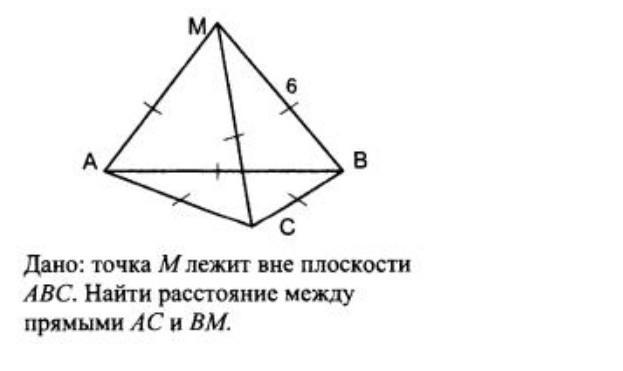
Дано: точка М лежит вне плоскости ABC. Найти расстояние между прямыми AC и ВМ.
Ответы
Ответ:
3
Объяснение:
Расстояние между прямыми — это длина перпендикуляра к этим прямым, соединяющего две точки этих прямых (одна точка на одной прямой, другая на другой).
Проведём ВН⊥АС, МН⊥АС (т.к. ΔАВС - равносторонний, то ВН и МН являются также медианами ⇒ АН=НС=МК=КВ=3см.)
Признак перпендикулярности прямой и плоскости: если прямая перпендикулярная к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
Т.к. АС перпендикулярна двум пересекающимся прямым плоскости (МНВ), то АС⊥(МНВ).
В ΔМНВ проведём высоту НК. НК⊥МВ.
Т.к. АС⊥(МНВ) ⇒ АС⊥ любой прямой (МНВ) ⇒ АС⊥НК
НК⊥МВ, АС⊥НК ⇒НК - перпендикуляр к обеим прямым. НК - искомое расстояние.
В ΔАВН найдём ВН по теореме Пифагора: ВН²=АВ²-АН²=36-9=27
В ΔМНВ найдём Высоту НК. Рассмотрим ΔВНК(∠К=90°), по т.Пифагора:
НК²=ВН²-КВ²=27-9=18
НК=√18=3√2 см