Предмет: Математика,
автор: danilova035690kou
1) Найдите производные первого и второго порядка
2) найдите производные первого и второго порядка . Напишите уравнение касательной в точке х0=2
1. У= х^3+6х^2+9х
2. У= х^2/х-2
Приложения:
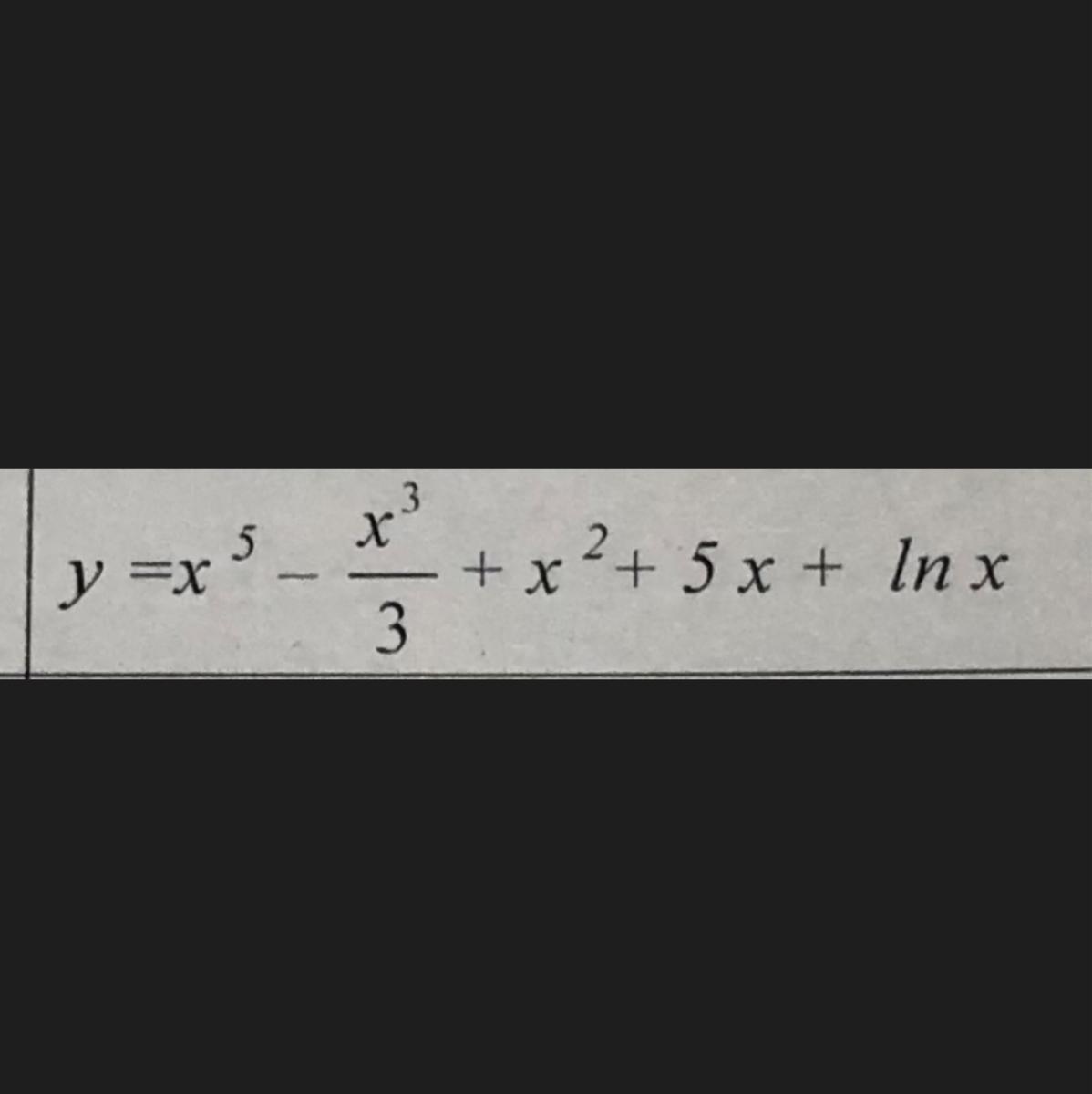
Ответы
Автор ответа:
0
Ответ:
в х0 = 2
1.
2.
danilova035690kou:
Огромное вам спасибо , очень помогли ❤️
Похожие вопросы
Предмет: Қазақ тiлi,
автор: carD1
Предмет: Русский язык,
автор: Ediks1998
Предмет: Математика,
автор: albinamaks15
Предмет: Геометрия,
автор: ТеЙнА
Предмет: Физика,
автор: beglec11