Предмет: Математика,
автор: N1CK111
Найдите производную функцию, помогите
Приложения:
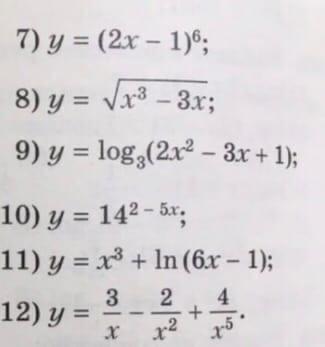
Ответы
Автор ответа:
1
7)
8)
9)
10)
11)
12)
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: yavovan98989
Предмет: Русский язык,
автор: irakova
Предмет: Химия,
автор: Andegraun
Предмет: Информатика,
автор: Dimka23124