Помогите срочно пожалуйста!!! Даю 30 баллов...

Ответы
1. Диагональ делит прямоугольник на прямоугольные треугольники, в которых катетами являются стороны прямоугольника, а диагональ - гипотенуза. По теореме Пифагора:
см.
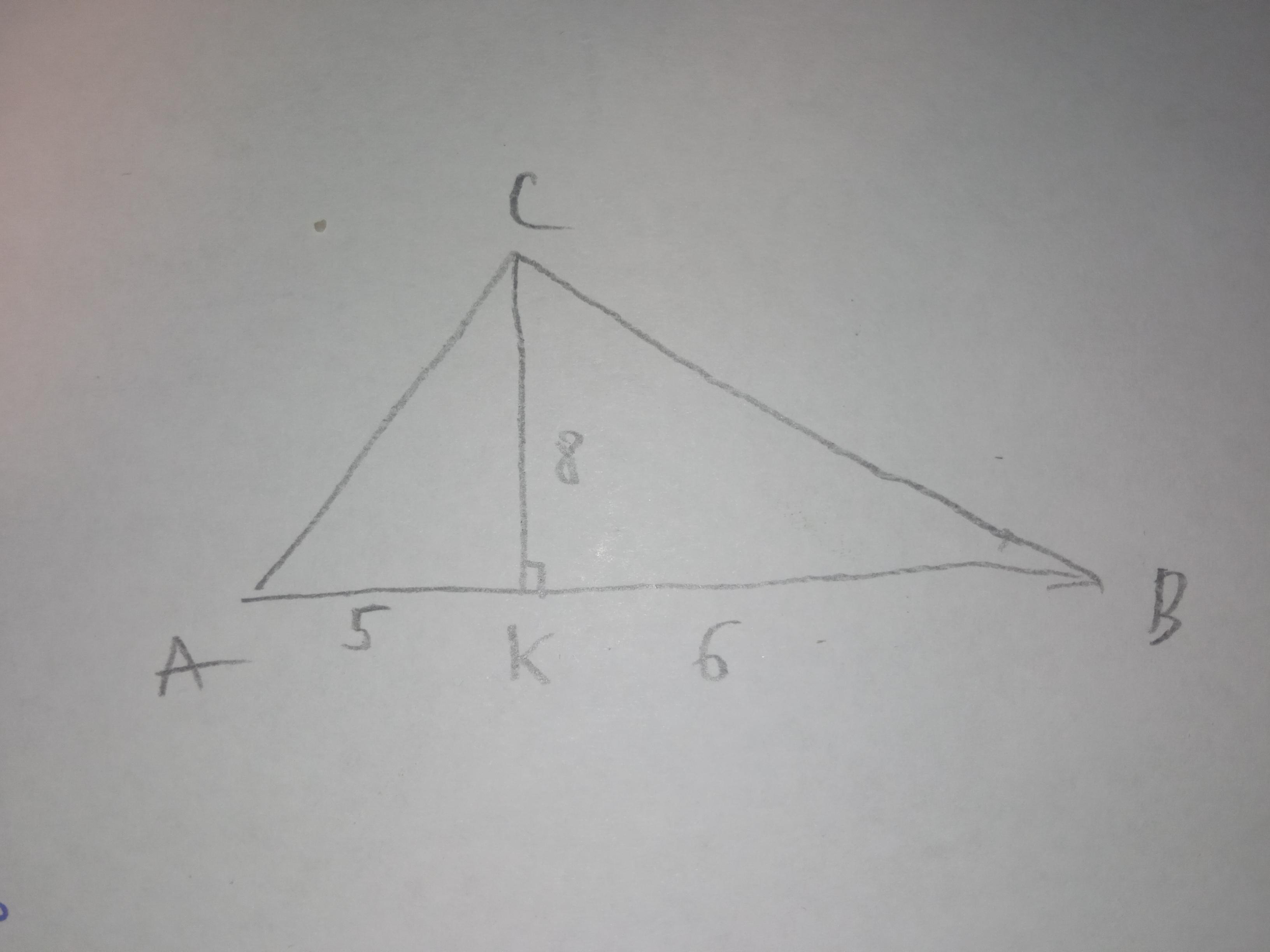
2. Здесь сразу можно вычислить дм. Высота делит треугольник на два прямоугольных треугольника. Рассмотрим каждый.
В катетами являются
и
, а
, сторона треугольника - гипотенуза. По теореме Пифагора:
дм.
В катетами являются
и
, а
, сторона треугольника - гипотенуза. По теореме Пифагора:
дм.
Решение:
1. Если нарисовать диагональ в прямоугольнике, то мы увидим, что образуются два прямоугольных треугольника, где диагональ будет гипотенузой, а длинна и ширина - катетами. Гипотенузу можно найти по теореме Пифагора: , где с - гипотенуза, a и b - катеты. Выходит, что диагональ прямоугольника равна:
см
2.
Высота дала нам два прямоугольных треугольника: ΔACK (∠CKA = 90°) и ΔCBK (∠CKB = 90°). Здесь нам нужно найти боковые стороны, которые являются гипотенузами треугольников. Так найдём же их, применив ту же теорему Пифагора! Имеем:
см
см