Предмет: Геометрия,
автор: davyskibadara
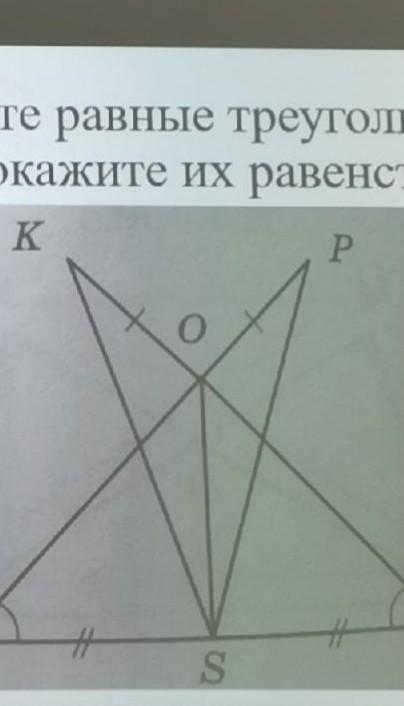
Докажите, что треугольник KOS= треугольнику POS, там справа буква M и слева буква N, где не видно. очень надо! (((
Приложения:
sonechkamarmeladova2:
Можно ли использовать св-во равнобедренной трапеции?
оу, мы это ещё не проходили(
равноб. тр-ка достаточно
углы при осн равны, значит MNO равноб., MS=SN, значит OS медиана, она же бисс. раз она бисс., значит уголMOS=NOS. уголKMO=PON как верт. значит их сумма KOS=POS. OS - общая сторона, значит искомые тр-ки равны
огромное спасибо!!!)))
пж))
Ответы
Автор ответа:
1
Объяснение:
рассмотрим KOS и POS
у них:
KO=PO по условию
OS - общая
рассмотрим NOM
у него:
угол N = углу M по условию, следовательно треугольник NOM - равнобедренный.
т.к. NS = MS, OS - биссектриса угла MON по свойству медианы равнобедренного треугольника, а значит угол MOS = углу NOS.
NO = MO как боковые стороны равнобедренного треугольника, следовательно угол KOS = POS.
следовательно треугольник POS = треугольнику KOS по двум сторонам и углу между ними
Похожие вопросы
Предмет: Русский язык,
автор: sasca163
Предмет: Математика,
автор: swetasimonenko
Предмет: Математика,
автор: jaster272
Предмет: Алгебра,
автор: раве
Предмет: История,
автор: zina111