Предмет: Математика,
автор: Oleg321875
Помогите математика 40 баллов
Приложения:
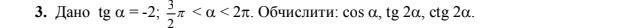
Ответы
Автор ответа:
2
Ответ:
угол принадлежит 4 четверти, синус и котангенс отрицательные, косинус положительный.
по формуле
Похожие вопросы
Предмет: Математика,
автор: llosos
Предмет: Алгебра,
автор: цилиндр1
Предмет: Математика,
автор: saryan168330
Предмет: Физика,
автор: robik308