Предмет: Математика,
автор: Аноним
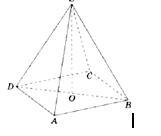
В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SО = 16, ВD = 40. Найдите боковое ребро SC
Приложения:
Ответы
Автор ответа:
1
Ответ: SC=4√16
решение:
SC=SA=SB=SD=40( по условию - пирамида правильная, значит все боковые рёбра равны)
Рассмотрим ΔSOB, так как пирамида правильная, то в основании квадрат, а BD- диагональ квадрата, Точка О- высота пирамиды делит диагональ пополам( ΔDSB- равнобедренный, SO- является высотой и медианой одновременно)
ОВ= BD:2=40:2=20
По теореме Пифагора найдём SB²=SO²+OB²
Аноним:
можешь тут помочь?
https://znanija.com/task/41520137
Похожие вопросы
Предмет: Английский язык,
автор: lera030430
Предмет: Математика,
автор: dasha3787
Предмет: Литература,
автор: kiralexandrov2
Предмет: Математика,
автор: irishka20111
Предмет: Математика,
автор: pasa12pasa