ДАЮ 30 БАЛЛОВ
Решите систему неравенств
Подробное решение
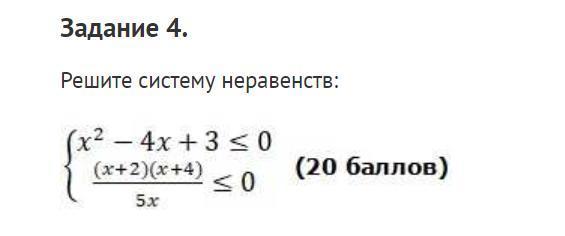
Ответы
x² - 4x + 3 = (x - 1)(x - 3)
Метод интервалов
(x - 1)(x - 3) ≤ 0
+++++++[1] ------------ [3]+++++++
x ∈ [1, 3]
(x + 2)(x + 4)/5x ≤ 0
------------[-4] +++++++++[-2] ------------ (0) ++++++++
x ∈ [-∞, -4] U [-2, 0)
пересекаем x ∈ [1, 3]
нет переcечений
x ∈ ∅
Ответ:
В решении.
Объяснение:
Решить систему неравенств:
х² - 4х + 3 <= 0
(x + 2)(x + 4)/5x <= 0
Решить первое неравенство.
Приравнять неравенство к нулю и решить как квадратное уравнение:
х² - 4х + 3 = 0
D=b²-4ac =16 - 12 = 4 √D=2
х₁=(-b-√D)/2a
х₁=(4 - 2)/2
х₁=2/2
х₁=1;
х₂=(-b+√D)/2a
х₂=(4 + 2)/2
х₂=6/2
х₂=3.
Теперь начертить СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= 1 и х= 3, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у <= 0 (график ниже оси Ох) при х∈[1; 3].
Неравенство нестрогое, скобки квадратные.
Решение первого неравенства х∈[1; 3].
Решить второе неравенство.
(x + 2)(x + 4)/5x <= 0
Приравнять неравенство к нулю и решить как квадратное уравнение.
(x + 2)(x + 4)/5x = 0
а) (x + 2)(x + 4) = 0
Можно раскрыть скобки и получить квадратное решение, потом найти через дискриминант х₁ и х₂.
А можно взять готовые значения х₁ и х₂ из уравнения:
х₁ = -2; х₂ = -4;
б) 5х = 0
х₃ = 0
Решение второго неравенства х∈(-∞; -4]∪[-2; 0).
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем значения -4, -2, 0, 1, 3.
х∈[1; 3] - штриховка вправо от 1 до 3.
х∈(-∞; -4]∪[-2; 0) - штриховка вправо от - бесконечности до -4 и
от -2 до 0.
Пересечения решений (двойной штриховки) нет.
Следовательно, решений системы неравенств нет.