Question

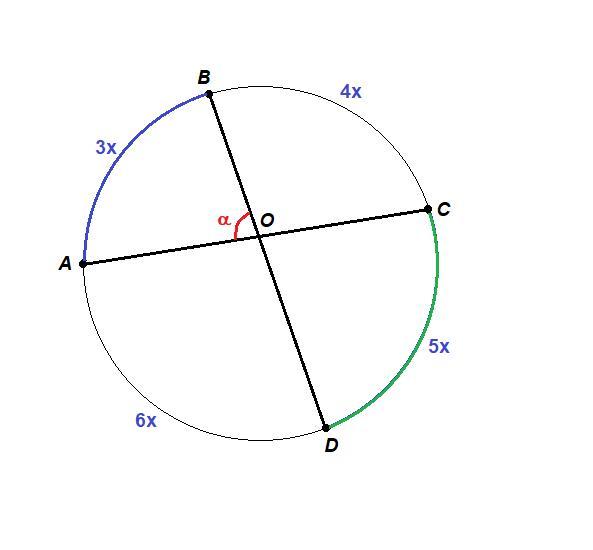
На окружности отметили точки A, B, C и D, которые делят её на
дуги AB, BC, CD AD, градусные меры
которых относятся как 3:4:5:6. Найдите угол между хордами AC и BD.

Answer 1

Ответ:

Угол между хордами AC и BD:

20°

Объяснение:

Чтобы найти угол между хордами, найдем градусные меры дуг.

Пусть х - коэффициент пропорциональности, тогда

∪АВ = 3х, ∪ВС = 4х, ∪CD = 5х, ∪AD = 6x.

Полная окружность составляет 360°.

3x + 4x + 5x + 6x = 360°

18x = 360°

x = 20°

∪АВ = 3 · 20° = 60°,

∪ВС = 4 · 20° = 80°,

∪CD = 5 · 20° = 100°,

∪AD = 6 · 20° = 120°

• Угол между хордами равен полуразности дуг, заключенных внутри этого угла и угла, вертикального данному.

$\alpha =\dfrac{\smallsmile CD\;-\smallsmile AB}{2}=\dfrac{100^\circ-60^\circ}{2}=20^\circ$