Предмет: Математика,
автор: buio44q
Даю сорок баллов, помогите решить. Подробное решение.
Приложения:
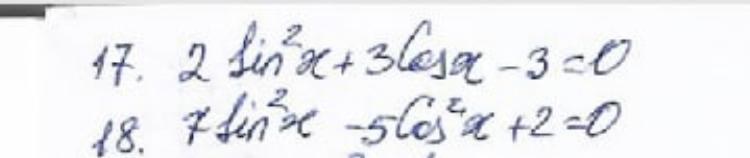
Ответы
Автор ответа:
1
Пошаговое объяснение:
17.
ОДЗ: x - любые
По основному тригонометрическому тождеству
Значит
Раскроем скобки
Приведем подобные и умножим все уравнение на - 1
Пусть
Получаем
Дискриминант равен
Корни
и
Значит,
Или
Оба корня входят в ОДЗ.
18.
ОДЗ: x - любые
Пусть
Тогда уравнение будет выглядеть
Приведем подобные, оставив переменные слева, а числа - справа:
Откуда
Тогда
Или
В первом случае
Во втором случае
Оба корня входят в ОДЗ.
Удачи!
В качестве благодарности сойдёт лайк и 5 звёзд!)))
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Математика,
автор: Lizashekina
Предмет: Математика,
автор: Ninzhurilko
Предмет: Английский язык,
автор: Аноним
Предмет: Химия,
автор: serzzzhant111
Предмет: Математика,
автор: alisabars071195