Предмет: Алгебра,
автор: olesechka2004
Решите пожалуйста систему неравенств:
Приложения:
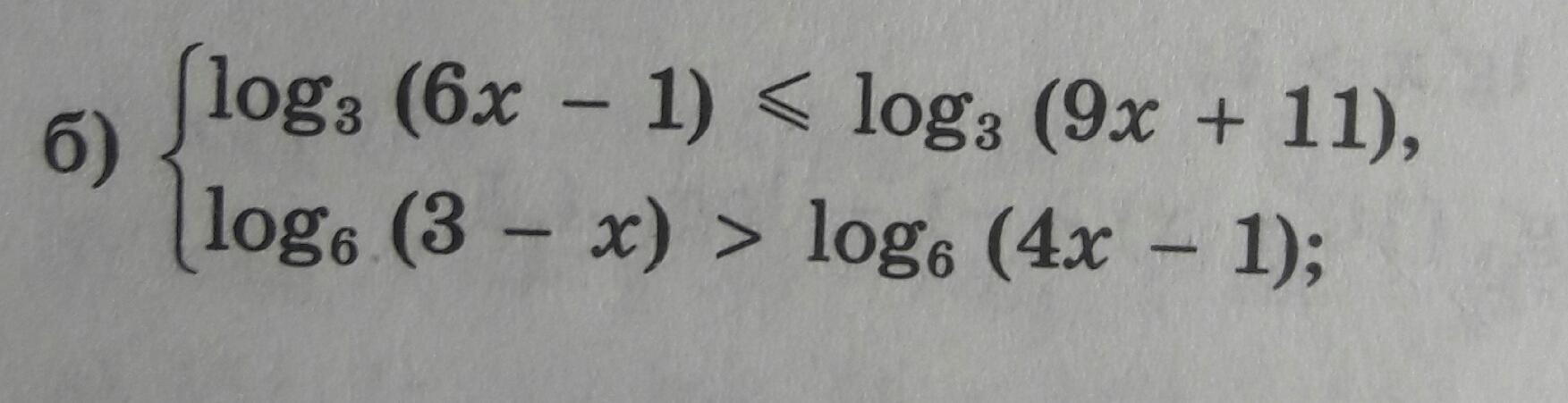
Ответы
Автор ответа:
1
Для начала найдём область допустимых значений переменной , учитывая все накладываемые на неё ограничения.
Продолжаем решать систему неравенств, но добавляем в неё наше новое ограничение.
Откуда получаем, что:
Veronika724:
Далее возврат к исходной системе. Логарифмы отбрасываются, поскольку основания логарифмов в верхнем и нижнем уравнении одинаковые, но при этом добавляется промежуток, о котором рассказано выше. Два простых неравенства решаются, а далее находится промежуток, удовлетворяющий всем трём неравенствам.
Если и после этого Вам что-то не понятно, то повторите определение логарифма и решение систем неравенств. Удачи.
В вашем решении почему то всё написано красными словами(begin,gathered и тд)
Понятия не имею, почему у Вас это так отображается. У меня и у моих знакомых всё замечательно.
Всё,разобралась.Оказывается это только в приложении так,а на сайте всё хорошо.
Спасибо большое!
Всегда пожалуйста, удачи в учёбе :))
Кстати, спасибо, что открыли мне глаза на решение этой проблемы.
Не за что)
Уже не в первый раз мне предъявляют, что мои ответы так выглядят. Теперь я хоть знаю, как это исправить :)
Похожие вопросы
Предмет: Химия,
автор: бобер45
Предмет: Математика,
автор: nastytany12
Предмет: Математика,
автор: rachenko84
Предмет: Химия,
автор: Лена150303