Предмет: Математика,
автор: skhekhekh
Помоги пожалуйста решить =(
Приложения:
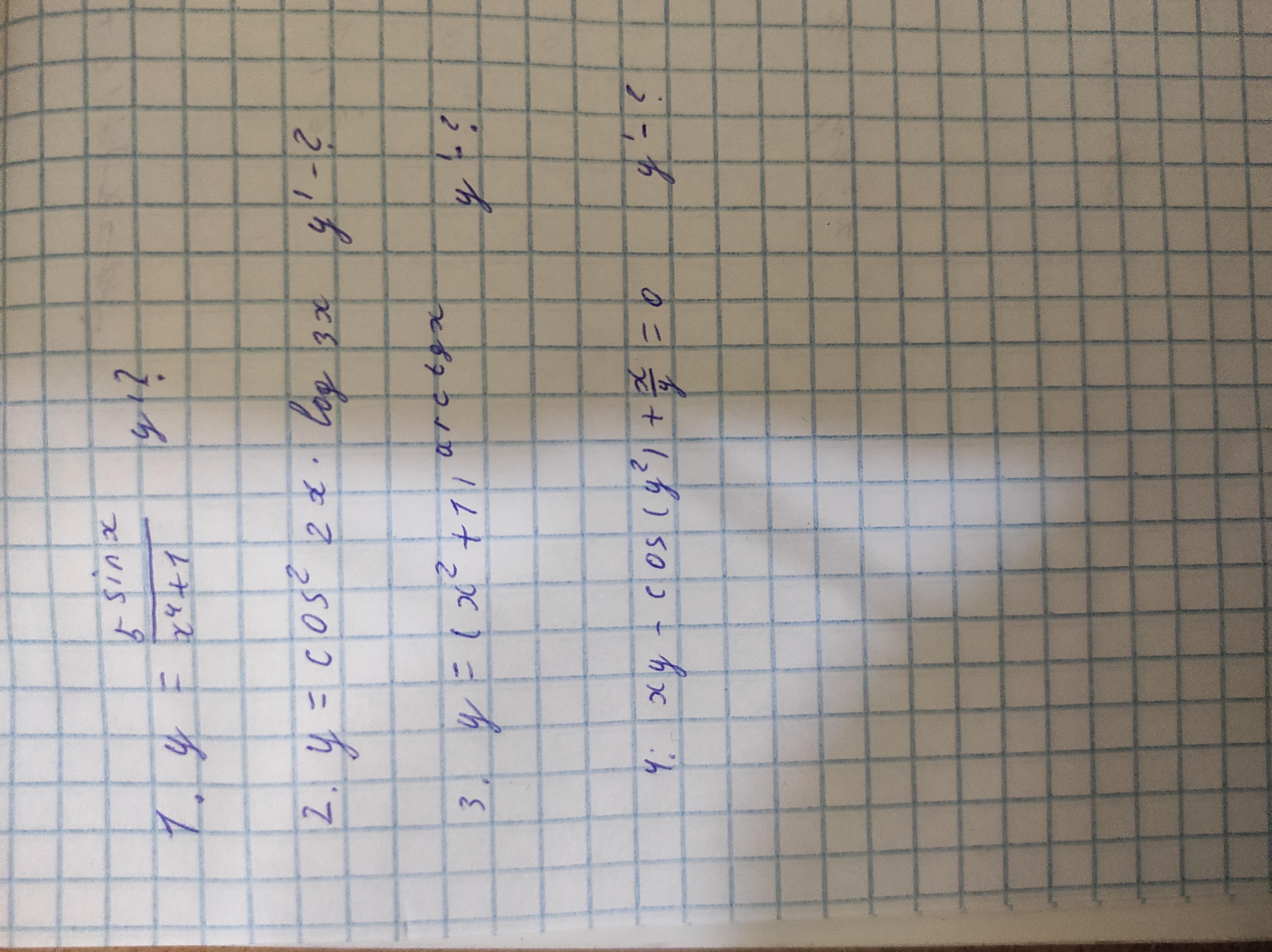
Ответы
Автор ответа:
2
Ответ:
1.
2.
3.
формула:
4.
lybkivskyiyra:
Помоги мне пожалуйста, если можешь.
Похожие вопросы
Предмет: Математика,
автор: nikitosino
Предмет: Русский язык,
автор: artamonelena
Предмет: Математика,
автор: merser0202
Предмет: Химия,
автор: alwaysb
Предмет: Математика,
автор: лена63613