Предмет: Алгебра,
автор: alex111207shadski
1 вариант пж очень надо
Приложения:
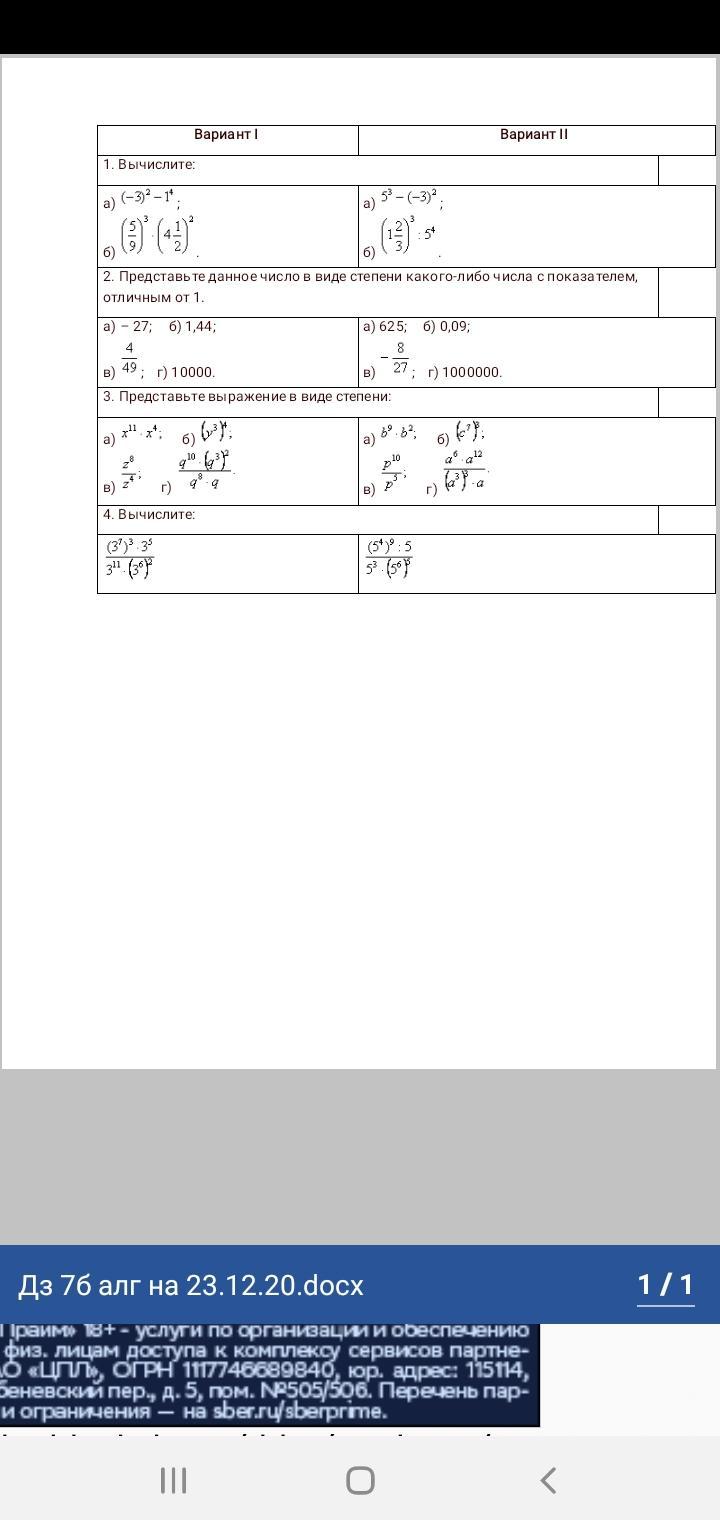
Ответы
Автор ответа:
1
1.
а)
б)
2.
а)
б)
в)
г)
3.
а)
б)
в)
г)
4)
Похожие вопросы
Предмет: История,
автор: sotirealty98
Предмет: Биология,
автор: SanyOkJK
Предмет: Математика,
автор: 69vd69
Предмет: Математика,
автор: fedia5
Предмет: Математика,
автор: Данил4532