Question

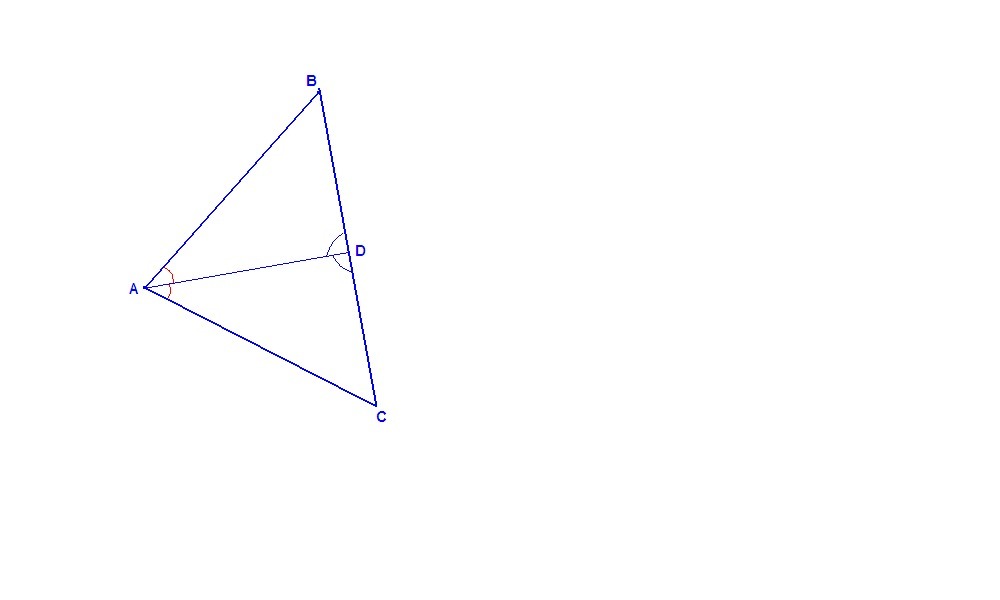
луч AD - биссектриса угла BAC. Докажите, что AB=AC, если известно, что углы ADB=ADC

Answer 1

1 способ:

∠ADB = ∠ADC по условию, эти углы смежные, значит их сумма равна 180°, тогда

∠ADB = ∠ADC = 180° : 2 = 90°.

Значит биссектриса AD является высотой, тогда ΔАВС равнобедренный по признаку ранобедренного треугольника, значит

АВ = АС.

2 способ:

∠BAD = ∠CAD, так как AD биссектриса,

∠ADB = ∠ADC по условию,

AD - общая сторона для треугольников ADB и ADC, значит

ΔADB = ΔADC по стороне и двум прилежащим к ней углам, ⇒

АВ = АС.