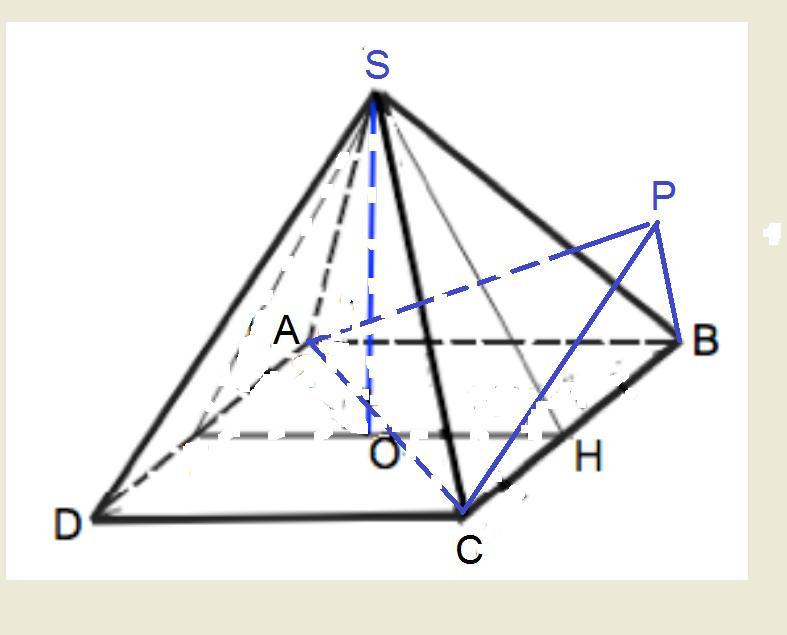
В правильной четырехугольной пирамиде SAВCD стороны основания и высота равны 2 см. Найдите угол между плоскостью SAB и прямой АС.
Ответы
Дана правильная четырехугольная пирамида SAВCD, сторона основания "а" и высота "Н" равны 2 см.
Эту задачу можно решит двумя способами - 1) геометрическим и 2) векторным.
1) Угол между плоскостью SAB и прямой АС - это угол между АС и её проекцией на плоскость SAB.
Апофема боковой грани А = √((a/2)² + H²) = √(1² + 2²) = √5.
Косинус угла наклона боковой грани к основанию равен: cos β = 1/√5.
Спроецируем точку С на плоскость SAB - пусть это точка Р.
ВР = a*cos β = 2*( 1/√5)= 2/√5.
Проекция АР = √(a² + BP²) = √(2² + ( 2/√5)²) = √(4 + (4/5)) = √(24/5).
Диагональ АС = 2√2 (по свойству гипотенузы в равнобедренном прямоугольном треугольнике).
Отрезок СР = a*sinβ.
Находим sinβ = √(1 - cos²β) = √(1 - (1/√5)²) = √(1 - (1/5)) = 2/√5.
СР = 2*(2/√5) = 4/√5.
Получили стороны треугольника, где угол САР и есть угол между АС и плоскостью SAB.
Решается по теореме косинусов.
cos CAP = ((√2)² + (√(24/5))² - (4/√5)²)/(2*√2*√(24/5)) = 0,774597.
Угол САР = 0,684719 радиан или 39,23152 градуса.