Предмет: Алгебра,
автор: qoew7
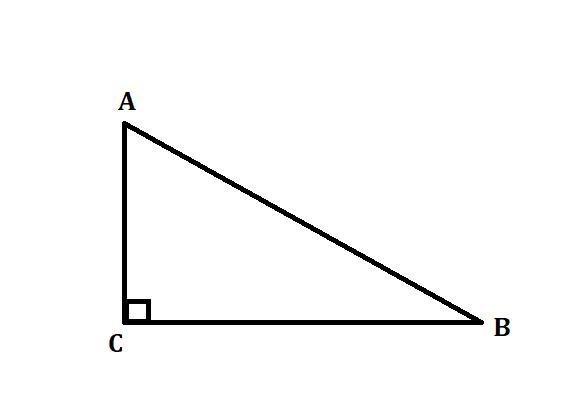
В треугольнике АВС угол С прямой, а стороны АС=8см и СВ=15см. Найдите синус и тангенс угла В.
Ответы
Автор ответа:
1
Ответ:
;
Объяснение:
- Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.
Найдём гипотенузу AB по теореме Пифагора:
см
- Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: НеуловимыйДвояшник
Предмет: Русский язык,
автор: ladka12
Предмет: Русский язык,
автор: русский151
Предмет: Биология,
автор: Ульяна285a