Question

Две стороны прямоугольного треугольника равны: 4 см и 12 см. Найдите третью сторону треугольника.
Рассмотрите все возможные случаи.
8 или 16
82 или 4/10
2/8 или 102
128 или 160

Answer 1

Ответ:

$8\sqrt{2}$ см или $4\sqrt{10}$ см

Пошаговое объяснение:

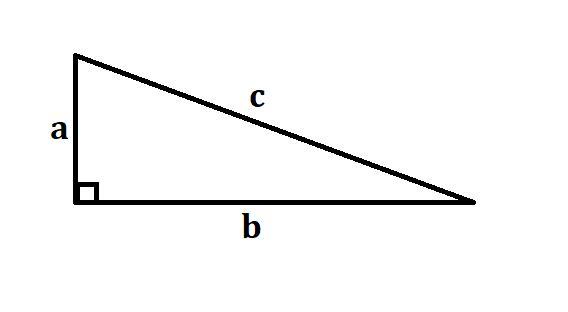
Здесь можно рассмотреть 2 случая: 1) 2 известные стороны - катеты данного прямоугольного треугольника, а 3 неизвестная сторона - гипотенуза данного прямоугольного треугольника; 2) 2 известные стороны - катет и гипотенуза данного прямоугольного треугольника, а 3 сторона - второй катет данного прямоугольного треугольника.

1 случай.

$a = 4$ см - катет прямоугольного треугольника

$b = 12$ см - катет прямоугольного треугольника

$c$ - гипотенуза прямоугольного треугольника

Найдём $c$ по теореме Пифагора:

$c^2 = a^2 + b^2 = 4^2 + 12^2 = 16 + 144 = 160$

$c = \sqrt{160} =4\sqrt{10}$ см

2 случай.

$a=4$ см - катет прямоугольного треугольника

$c = 12$ см - гипотенуза прямоугольного треугольника

$b$ - катет прямоугольного треугольника

Найдём $b$ по теореме Пифагора:

$b^2 = c^2 - a^2 = 12^2 - 4^2 = 144 - 16 = 128$

$b = \sqrt{128} = 8\sqrt{2}$ см