Предмет: Геометрия,
автор: ktototato
Решите 5 задачу,пожалуйста
Приложения:

Ответы
Автор ответа:
1
Ответ:
Объяснение:
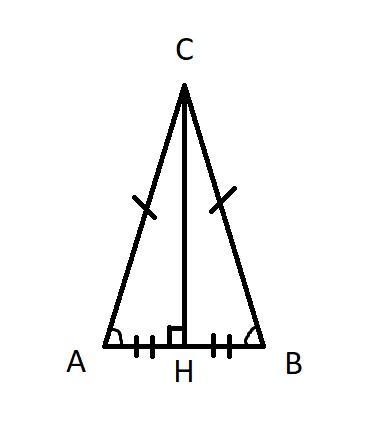
Опустим высоту из вершины C на основание AB. Обозначим эту высоту как CH. Так как треугольник ABC — равнобедренный, то высота также является медианой ⇒
Рассмотрим треугольник CAH. Так как ∠CHA = 90°, то треугольник CAH — прямоугольный. Угол при основании — это ∠CAH. Он равен 30° и является прилежащим к меньшему катету треугольника CAH ⇒
Приложения:
Похожие вопросы
Предмет: Математика,
автор: санчес2003
Предмет: Русский язык,
автор: ЛизаОдинцова
Предмет: Другие предметы,
автор: innamas79
Предмет: Алгебра,
автор: Ксюхахаха
Предмет: Биология,
автор: Богдан1221В