Предмет: Математика,
автор: Andrei00989
Первообразованная! Решите 1 вариант!!! С поиснениями за 10 минут!!
Приложения:
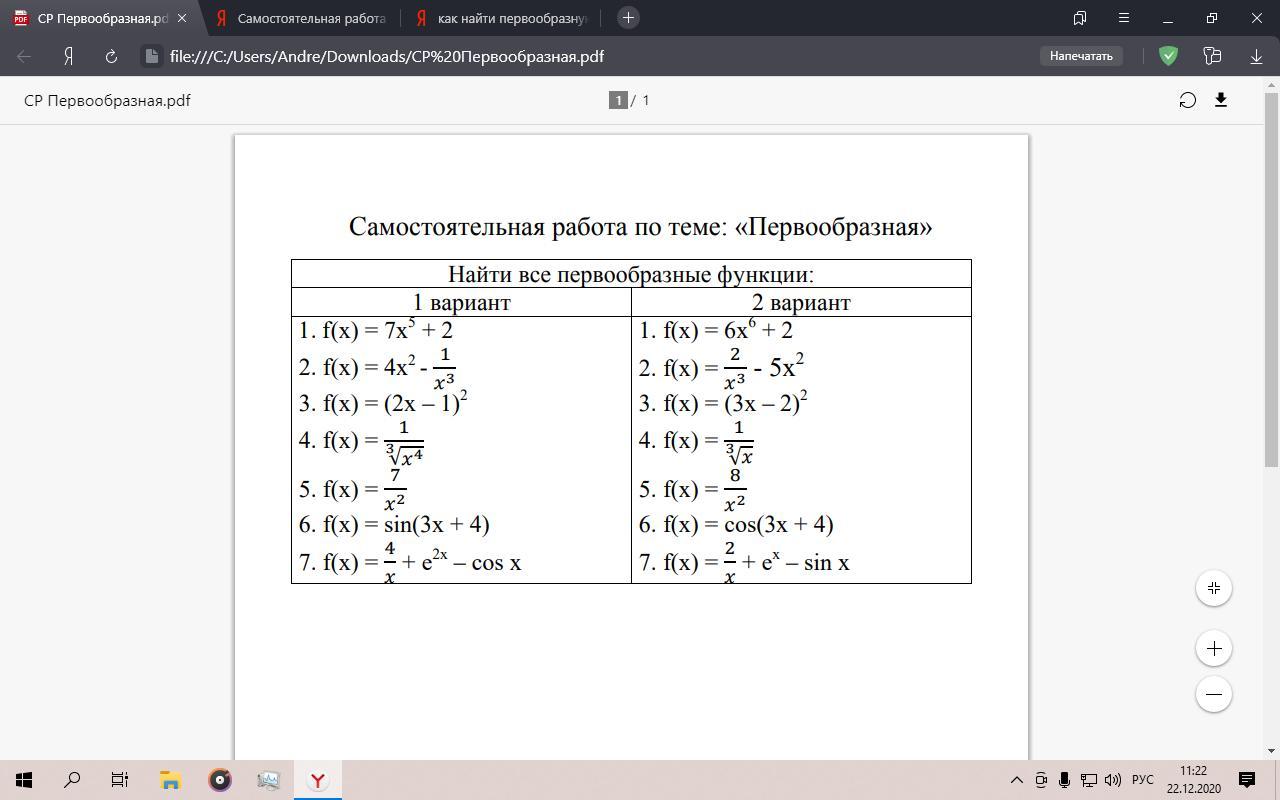
Ответы
Автор ответа:
2
1 вариант
2 вариант
Похожие вопросы
Предмет: Биология,
автор: ivan135q
Предмет: Физика,
автор: дашасмит
Предмет: Українська мова,
автор: Аноним
Предмет: Химия,
автор: КайргалиевКайрат
Предмет: Биология,
автор: татьяна20062309