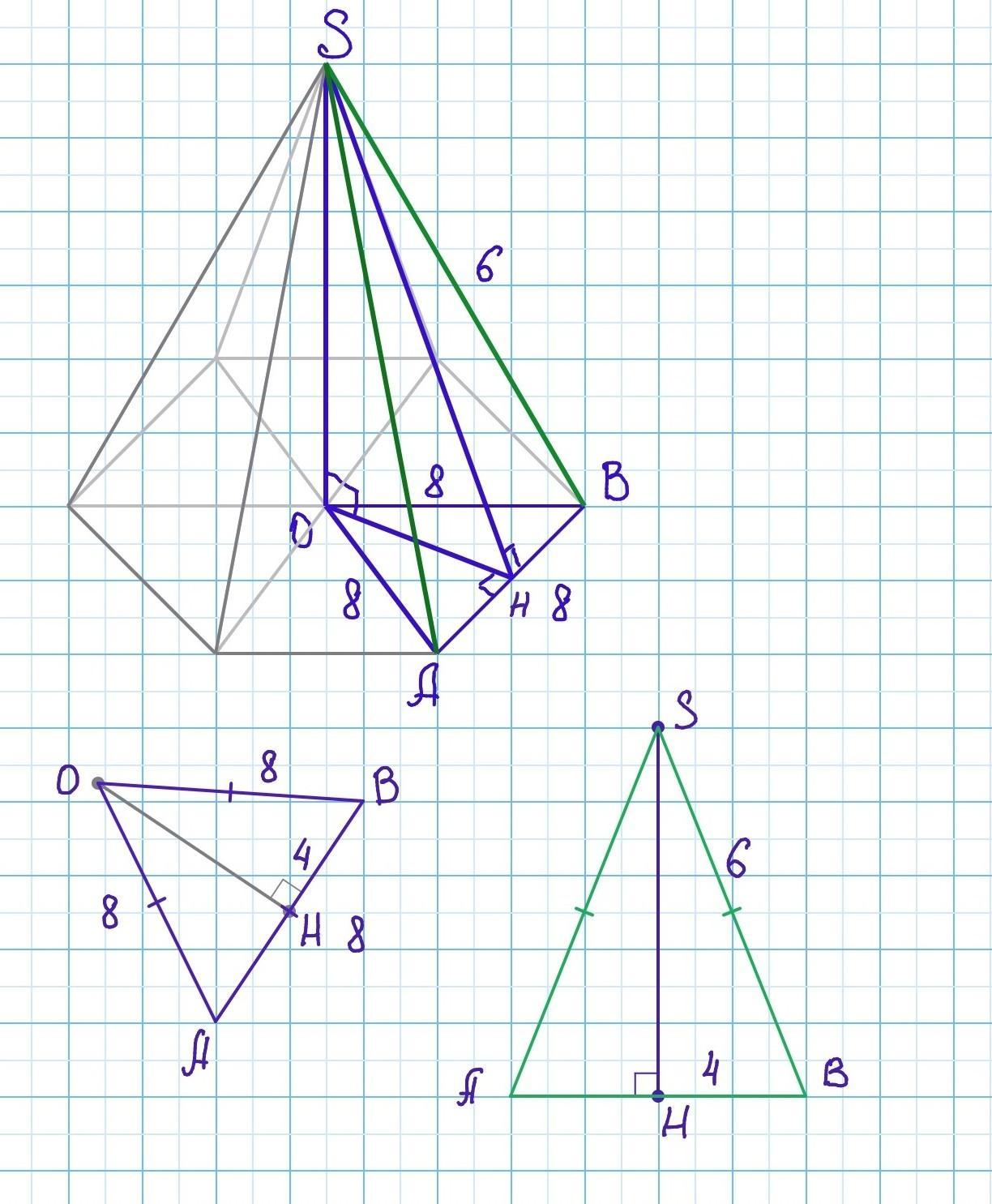
помогите пж
Боковое ребро правильной шестиугольной пирамиды SABCDEF равна 6 см. Радиус
окружности, описанной около основания пирамиды, равен 8 см.
Найдите площадь полной поверхности пирамиды.
Ответы
Ответ:
см²
Объяснение:
Для нахождения полной площади поверхности пирамиды нужно сложить площадь боковой поверхности и площадь основания.
1) Найдём площадь основания.
Основанием является правильный шестиугольник. Площадь правильного шестиугольника находим по формуле:
где а - сторона шестиугольника. В правильном шестиугольнике сторона = радиусу описанной окружности. => а=8 см.
Следовательно площадь основания Sосн:
см²
2) Найдём площадь боковой поверхности.
Sбок= ½ × Росн×SH
Pосн =6×а= 6×8=48 см - периметр основы.
SH - апофема.
SH⟂AB
SO⟂ОН, как высота пирамиды,=> по теореме о трёх перпендикулярах ОН⟂АВ.
В правильной пирамиде боковые грани - равнобедренные треугольники. SH- высота и медиана одного из них. Найдём SH по теореме Пифагора из прямоугольного треугольника SHB :
см
Sбок:
см²
3) Sп= Sосн+Sб
см²