Предмет: Геометрия,
автор: andreoskar12
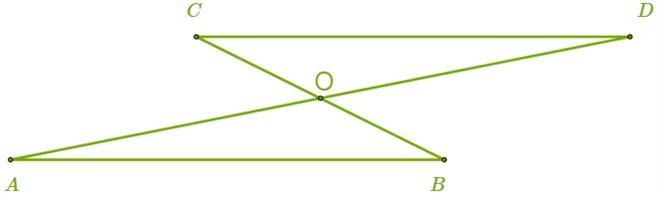
Точка пересечения O — серединная точка для обоих отрезков AD и BC.
Найди величину сторон AB и BO в треугольнике ABO, если DC = 39,1 см и CO = 16,8 см
(При ответе упорядочи вершины таким образом, чтобы углы при них были попарно равны.)
А. Так как отрезки делятся пополам, то
1. сторона BO в треугольнике ABO равна стороне
в треугольнике DCO;
2. сторона AO в треугольнике ABO равна стороне
в треугольнике DCO.
Угoл BOA равен углу
как вертикальный угол.
Треугольники равны по первому признаку равенства треугольников.
В равных треугольниках соответствующие стороны равны.
AB =
см;
BO =
см.
Приложения:
Ответы
Автор ответа:
7
Ответ:
AB = 39,1 см
BO = 16,8 см
Объяснение:
Дано: AO = OD, CO = BO, DC = 39,1 см, CO = 16,8 см
Найти: AB,BO - ?
Решение: Треугольник ΔAOB = ΔDCO по первому признаку равенства треугольников, так как по условию AO = OD, CO = BO, а угол ∠AOB = ∠COD как вертикальные углы. Так как треугольник ΔAOB = ΔDCO, то соответствующие элементы треугольников равны, тогда
AB = CD = 39,1 см, BO = CO = 16,8 см.
Похожие вопросы
Предмет: Математика,
автор: olesyagribanova
Предмет: Математика,
автор: мама8585
Предмет: Русский язык,
автор: smoroxin
Предмет: История,
автор: Sasha19551