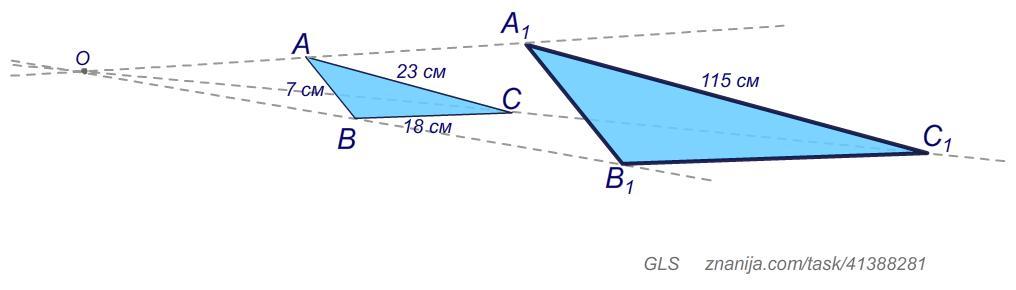
Треугольник ABC в гомотетии отображается в треугольник A1B1C1.
AB= 7 см;
BC= 18 см;
AC= 23 см.
Найди длины сторон треугольника A1B1C1, если длина длинной стороны этого треугольника равна 115 см.
Ответы
Ответ:
Длины сторон ΔA₁B₁C₁ :
A₁C₁ = 115 см; A₁B₁ = 35 cм; B₁C₁ = 90 cм.
Объяснение:
Гомотетия — это преобразование подобия с заданным центром в некоторой точке O и коэффициентом k, при котором каждая точка X отображается в точку X₁ так, что выполняется равенство: OX = k·OX₁.
При гомотетии получают новую фигуру, подобную данной с коэффициентом подобия k.
Две фигуры называются подобными, если у них соответствующие углы равны и соответствующие стороны пропорциональны.
ΔABC в гомотетии отображается в ΔA₁B₁C₁.
Известны стороны ΔABC: AB = 7 см; BC = 18 см; AC = 23 см.
Наибольшая сторона ΔABC пропорциональна наибольшей стороне ΔA₁B₁C₁.
Сторона AC = 23 см, пропорциональна стороне A₁C₁, ⇒ A₁C₁ = 115 см.
Найдем коэффициент подобия треугольников.
Каждая сторона ΔA₁B₁C₁ в 5 раз больше соответствующей стороны ΔABC.
A₁B₁ = 5AB = 5 · 7 см = 35 cм.
B₁C₁ = 5BC = 5 · 18 см = 90 cм.