Предмет: Алгебра,
автор: marikiri01
Найти неопределённый интеграл, результат проверить дифференцированием:
Приложения:
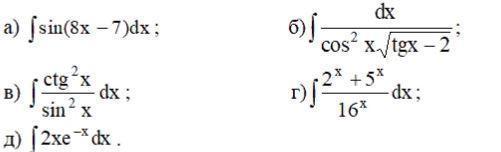
Ответы
Автор ответа:
1
marikiri01:
Подробнее можно?
Нужно расписать и проверить,вы не сделали
Похожие вопросы
Предмет: Английский язык,
автор: 0ника73
Предмет: Русский язык,
автор: Ангел3et
Предмет: Геометрия,
автор: 08923655mama
Предмет: Математика,
автор: Svetka201714