Предмет: Алгебра,
автор: filinhut
СРочно!!! пж очень срочно
Приложения:

Ответы
Автор ответа:
2
Ответ: (4;4), (2;6)
Объяснение:
Во вложении
Приложения:
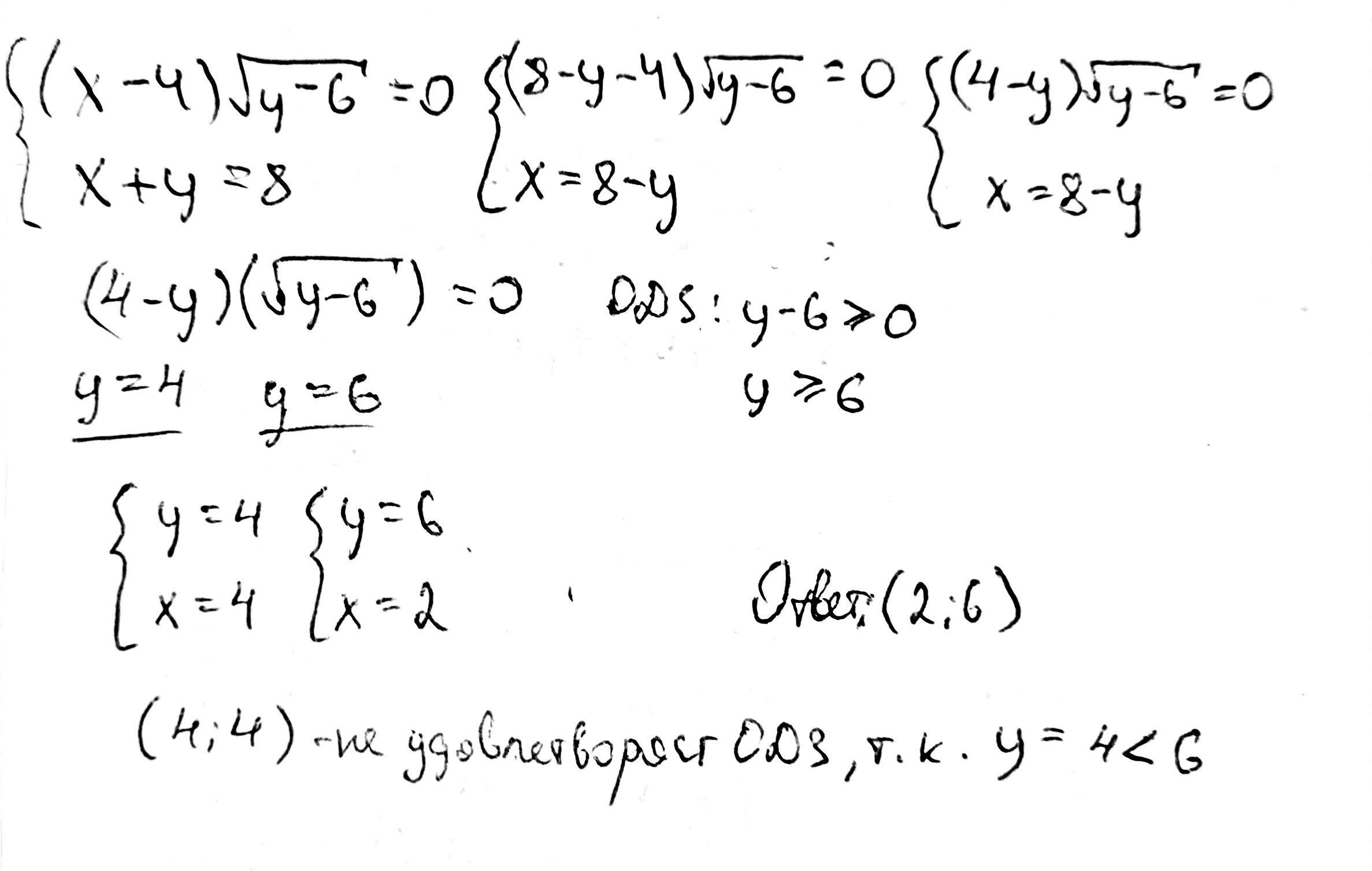
Автор ответа:
0
Ответ:
Объяснение:
ОДЗ:
Решение:
Пара (4; 4) не удовлетворяет ОДЗ, так как
Остаётся пара
Похожие вопросы
Предмет: Математика,
автор: Артём127
Предмет: История,
автор: Ptaok342
Предмет: Математика,
автор: fanfer
Предмет: Физика,
автор: Poprt
Предмет: Математика,
автор: gleb29ru