Question

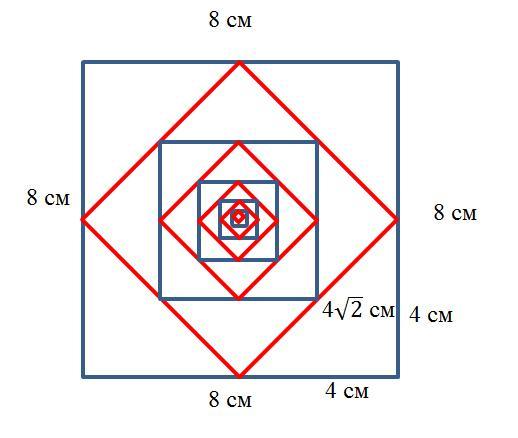
Квадрат длина стороны которого равна 8 см вписан другой квадрат вершинами которого являются середины сторон данного квадрата. В полученный квадрата таким же способом вписан другой квадрат и так далее. Найдите значение суммы периметров и значение суммы площадей этих квадратов​

Answer 1

Ответ:

Сумма периметров всех квадратов равна 64+32$\sqrt{2}$ см

Сумма площадей всех квадратов равна 128 см²

Объяснение:

Нужно знать:

1) Периметр P квадрата со стороной a:    P = 4·a.

2) Площадь S квадрата со стороной a:     S = a².

3) Гипотенуза c равностороннего треугольника с катетами a: c = a$\sqrt{2}$.

4) Сумма S всех членов бесконечно убывающей геометрической прогрессии с первым членом b₁ и знаменателем q определяется по формуле

$\tt S = \dfrac{b_1}{1-q}.$

Решение. Заметим, что длина стороны каждого вписанного квадрата определяется как гипотенуза равностороннего треугольника с катетами длиной равными половине длины стороны внешнего квадрата (см. рисунок).

По этой закономерности определяем стороны квадратов:

b₁ = 8, b₂ = 4$\sqrt{2}$, b₃ = 4, b₄ = 2$\sqrt{2}$, b₅ = 2, ...

Значит, стороны вписанных квадратов образуют бесконечно убывающую геометрическую прогрессию с первым членом b₁ = 8 см и знаменателем q = 1/$\sqrt{2}$ < 1.

Тогда периметры вписанных квадратов образуют следующую последовательность:

P₁= 4·8 = 32, P₂= 4·4$\sqrt{2}$ = 16$\sqrt{2}$, P₃= 4·4 = 16, P₄= 4·2$\sqrt{2}$ = 8$\sqrt{2}$, P₅= 4·2= 8, ...

Значит, по этой закономерности видно, что периметры вписанных квадратов образуют бесконечно убывающую геометрическую прогрессию с первым членом b₁ = 32 см и знаменателем q = 1/$\sqrt{2}$ < 1. Тогда сумма периметров всех квадратов равна

$\tt S(P) = \dfrac{32}{1-\dfrac{1}{\sqrt{2} } }=\dfrac{32}{\dfrac{\sqrt{2} -1}{\sqrt{2} } }=\dfrac{32\sqrt{2} }{\sqrt{2} -1 }=\dfrac{32\sqrt{2} \cdot (\sqrt{2} +1)}{(\sqrt{2} -1) \cdot (\sqrt{2} +1) }=\\\\=\dfrac{32\sqrt{2} \cdot (\sqrt{2} +1)}{(2 -1) }=32\sqrt{2} \cdot (\sqrt{2} +1)=64+32\sqrt{2} \;CM.$

Далее, площади вписанных квадратов образуют следующую последовательность:

S₁= 8² = 64, S₂= (4$\sqrt{2}$)² = 32, S₃= 4² = 16, S₄= (2$\sqrt{2}$)² = 8, S₅= 2²= 4, ...

Поэтому площади вписанных квадратов образуют бесконечно убывающую геометрическую прогрессию с первым членом b₁ = 64 см и знаменателем q = 1/2 < 1. Тогда сумма площадей всех квадратов равна

$\tt S(S) = \dfrac{64}{1-\dfrac{1}{2} }=\dfrac{64}{\dfrac{2 -1}{2 } }=\dfrac{64 \cdot 2 }{2 -1 }= 128 \;CM^2.$