Предмет: Алгебра,
автор: ilona4911
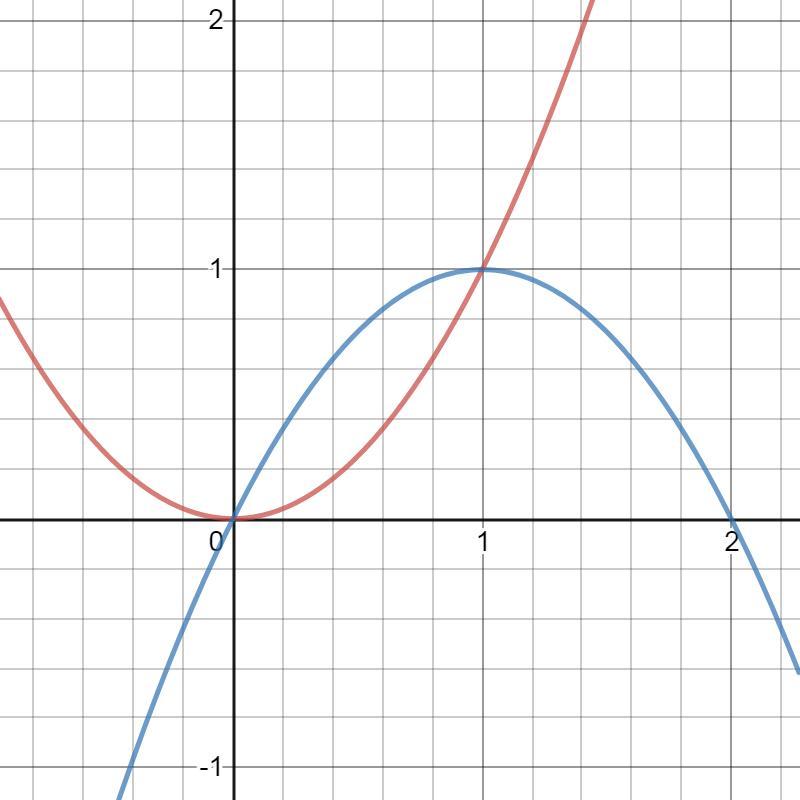
Запишіть площу фігури, обмеженої параболами y=x² і y=2x-x²
Ответы
Автор ответа:
2
Объяснение:
Ответ: S=0,3333 кв. ед.
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: lerasait
Предмет: Русский язык,
автор: vipolga2012
Предмет: Українська література,
автор: natali19671
Предмет: Геометрия,
автор: oleyniklilija1
Предмет: Химия,
автор: Cavosta1