Предмет: Математика,
автор: daniilanosov3
Помогите, пожалуйста с математикой. Нужно найти производную. Задание на фото
Приложения:
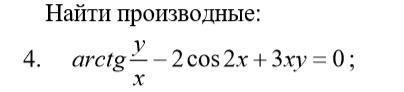
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: qristin
Предмет: Русский язык,
автор: lapik7575
Предмет: Математика,
автор: ViktiriaProtasova
Предмет: Математика,
автор: loxubejtemenya
Предмет: Алгебра,
автор: Karandashidze