Предмет: Геометрия,
автор: veronikadovzhenko15
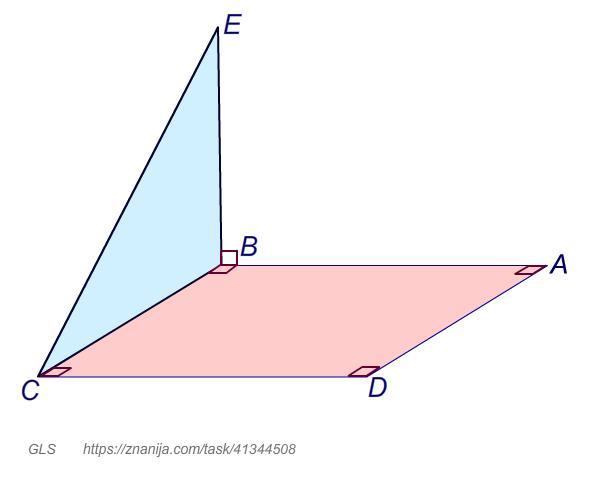
треугольник BCE и прямоугольник ABCD не лежат в одной плоскости. Угол ABE=90градусов. Доказать, что прямая DC перпендикулярна плоскости BCE и прямая АВ перпендикулярна прямой ЕС
Ответы
Автор ответа:
3
Ответ:
Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, то она перпендикулярна этой плоскости.
По условию ∠ABE = 90°, тогда AB ⊥ BE;
ABCD прямоугольник, AB⊥BC.
Отрезки BE и BC принадлежат плоскости ΔBEC.
Тогда АВ перпендикулярна плоскости ΔBCE.
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
⇒ AB перпендикулярна CE.
Если одна из двух параллельных прямых перпендикулярна к плоскости, то и вторая прямая перпендикулярна к плоскости.
AB ║ CD по свойству прямоугольника, и AB ⊥ плоскости ΔBCE , значит DC ⊥ плоскости ΔBCE.
Доказано.
Приложения:
Похожие вопросы
Предмет: Химия,
автор: kotmay5
Предмет: Математика,
автор: Burkova1lv
Предмет: Алгебра,
автор: artursavelev5
Предмет: Математика,
автор: milashra
Предмет: Алгебра,
автор: julianakas