Question

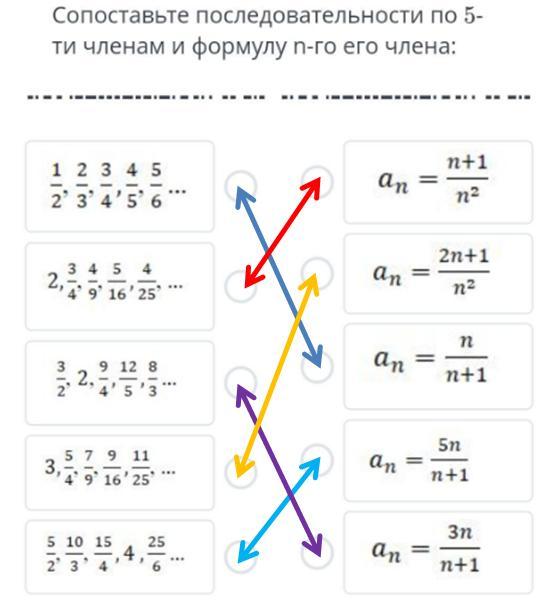
сопоставьте последовательности по 5-ти членам и формулу n-го его члена:

Answer 1

Ответ и Объяснение:

Каждый член последовательностей разложим по порядковым номерам и определяем закономерность (см. рисунок).

$\tt a_1 = \dfrac{1}{2} = \dfrac{1}{1+1}\\\\a_2 = \dfrac{2}{3}=\dfrac{2}{2+1} \\\\a_3 = \dfrac{3}{4}=\dfrac{3}{3+1}\\\\a_4 = \dfrac{4}{5} =\dfrac{4}{4+1}\\\\a_5 = \dfrac{5}{6} =\dfrac{5}{5+1}\\...\\a_n=\dfrac{n}{n+1}.$

$\tt a_1 =2= \dfrac{1+1}{1^2}\\\\a_2 =\dfrac{3}{4} =\dfrac{2+1}{2^2} \\\\a_3 =\dfrac{4}{9}=\dfrac{3+1}{3^2}\\\\a_4 =\dfrac{5}{16} =\dfrac{4+1}{4^2}\\\\a_5 =\dfrac{6}{25} =\dfrac{5+1}{5^2}\\...\\a_n=\dfrac{n+1}{n^2}.$

$\tt a_1 =\dfrac{3}{2} = \dfrac{3 \cdot 1}{1+1}\\\\a_2 =2=\dfrac{3 \cdot 2}{2+1} \\\\a_3 =\dfrac{9}{4}=\dfrac{3 \cdot 3}{3+1}\\\\a_4 =\dfrac{12}{5} =\dfrac{3 \cdot 4}{4+1}\\\\a_5 =\dfrac{8}{3} =\dfrac{3 \cdot 5}{5+1}\\...\\a_n=\dfrac{3 \cdot n}{n+1}.$

$\tt a_1 =3 = \dfrac{2 \cdot 1+1}{1^2}\\\\a_2 =\dfrac{5}{4} =\dfrac{2 \cdot 2+1}{2^2} \\\\a_3 =\dfrac{7}{9}=\dfrac{2 \cdot 3+1}{3^2}\\\\a_4 =\dfrac{9}{16} =\dfrac{2 \cdot 4+1}{4^2}\\\\a_5 =\dfrac{11}{25} =\dfrac{2 \cdot 5+1}{5^2}\\...\\a_n=\dfrac{2 \cdot n+1}{n^2}.$

$\tt a_1 =\dfrac{5}{2} = \dfrac{5 \cdot 1}{1+1}\\\\a_2 =\dfrac{10}{3} =\dfrac{5 \cdot 2}{2+1} \\\\a_3 =\dfrac{15}{4}=\dfrac{5 \cdot 3}{3+1}\\\\a_4 =4 =\dfrac{5 \cdot 4}{4+1}\\\\a_5 =\dfrac{25}{6} =\dfrac{5 \cdot 5}{5+1}\\...\\a_n=\dfrac{5 \cdot n}{n+1}.$