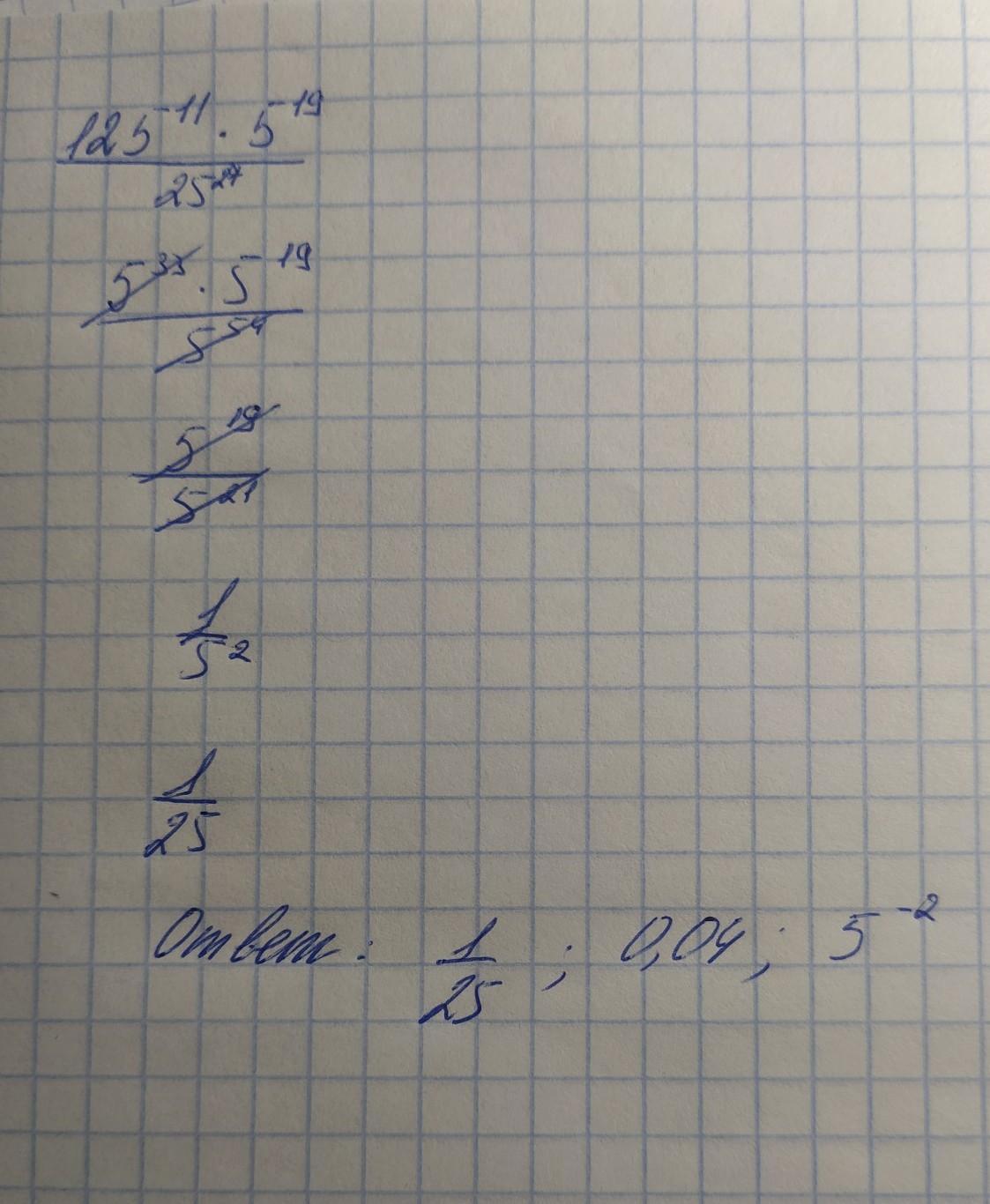Question

Решите пожалуйста! Алгебра

Answer 1

Объяснение:

Задача 1.

а)

${5}^{4} = 625$

б)

$( { -7})^{3} = - 343$

в)

$( - 1 \times \frac{1}{3})^{2} = ( - \frac{4}{3})^{2} = \frac{16}{9}$

г)

$(1.5)^{3} = ( \frac{3}{2} )^{2} = \frac{27}{8}$

Задача 2.

а)

$5^{98} \times {5}^{32} = {5}^{98 + 32} = {5}^{130}$

б)

$5^{80}$

г)

$5^{210 - 40} = {5}^{170}$

Задача 3.

а)

$(0.4)^{6} \times 5^{6} = (0.4 \times 5)^{6} = {2}^{6} = 64$

б)

проблематично решение записать, но,

${5}^{23 - 25} = \frac{1}{5}$

в знаменателе пишется

${5}^{2}$

и получается

$\frac{1}{25}$

или ответ можно записать как

$0.04$

а ещё и

${5}^{ - 2}$

Задача 4.

я записала их в том порядке, как нужно, то есть, по возрастанию

$- \frac{9}{43} = - 0.209302$

$- \frac{9}{215} = - 0.0418605$

$(0.2)^{3} = 0.008$

$( \frac{5}{6} )^{2} = \frac{25}{36} = 0.694$

Задача 6.

а) перенести в скобки члены с равным показателем степеней.

$(0.8 \times 1.25)^{100}$

умножаем числа

$1^{100}$

1 в любой степени равен исходному числу, точнее, 1.

Ответ: 1

б) записываем выражение в виде степени с основанием 5.

${125}^{11} = {5}^{33}$

${5}^{19} = {5}^{19}$

${25}^{27} = {5}^{54}$

нужно теперь упростить выражение.

${5}^{54 - 33} = {5}^{21}$

так же повторяем с другой частью

${5}^{21 - 19} = {5}^{2}$

и ответ

$\frac{1}{25}$

но можно записать в двух видах, это

1.

$0.04$

2.

${5}^{ - 2}$

фото решения, чтобы уж понять точно, я прикреплю

Задача 7.

а)

${16}^{28} \div {8}^{8}$

запишем выражение в виде степени с основанием два.

${2}^{112} \div {2}^{24}$

ответ получается

${2}^{88}$

и таким образом, мы сравниваем что больше, что меньше. Ответ конечно ясный, так как

${2}^{88}$

куда больше чем

${2}^{20}$

Ответ:

${2}^{88} > {2}^{20}$

к задаче 8, я прикреплю фото с объяснением