Предмет: Алгебра,
автор: sponazyrev
В правильный треугольник со стороной 10 см вписан другой треугольник, вершины которого находятся на серединах сторон данного треугольника, в этот треугольник таким же образом вписан следующий треугольник и так далее до бесконечности. Вычисли сумму площадей всех треугольников.
ОНЛАЙН МЕКТЕП ЗАДАНИЕ 6
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Площадь правильного треугольника со стороной a определяется по формуле
Сторона первого треугольника равна 10 см и поэтому его площадь равна
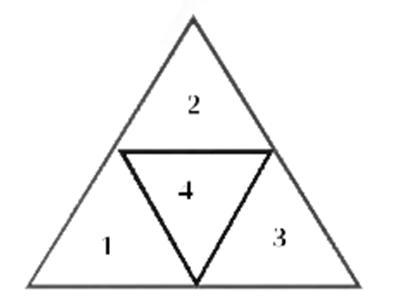
Далее, стороны треугольника, вершины которого находятся на серединах сторон внешнего треугольника являются средними линиями и по свойству средних линий внешний треугольник делится на 4 равных треугольников (см. рисунок). Значит площадь каждого внутреннего треугольника равна четверти внешнего треугольника.
В силу вышесказанного получим сумму площадей треугольников:
В итоге получили бесконечно убывающую геометрическую прогрессию первым членом равным и знаменателем
Сумма бесконечно убывающей геометрической прогрессии определяется по формуле:
Теперь вычислим сумму площадей всех треугольников:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: frgwerqgr
Предмет: География,
автор: НаСтЕнА010101
Предмет: Математика,
автор: leonidova13
Предмет: Алгебра,
автор: ангел769
Предмет: Алгебра,
автор: resensshow