Question

Диагонали ромба равны 12 см и 16 см. Найди высоту ромба.​

Answer 1

Ответ:

9,6 см.

Объяснение:

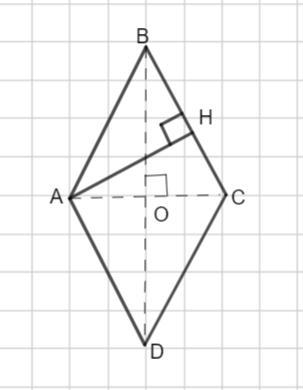
Пусть дан ромб ABCD.

Найдем площадь ромба по формуле:

$S=\dfrac{1}{2} d{_1}\cdot d{_2} ,$

где  $d{_1},d{_2}$ - диагонали ромба.

$S= \dfrac{1}{2} \cdot12\cdot16=6\cdot16=96$ см ².

Так как диагонали ромба пересекаются и точкой пересечения делятся пополам, то АО=ОС= 12:2=6 см.

BO=OD= 16 : 2=8 см.

Диагонали ромба пересекаются под прямым углом. Тогда

Δ ВОС - прямоугольный.

Найдем гипотенузу по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$BC^{2} =BO ^{2} +OC ^{2} ;\\BC= \sqrt{BO ^{2} +OC ^{2} } ;\\BC= \sqrt{8^{2} +6^{2} } =\sqrt{64+36} =\sqrt{100} =10$

Значит, сторона ромба равна 10 см.

Площадь ромба можно определить как произведение стороны на высоту, проведенную к стороне.

$S= BC\cdot AH;\\\\AH= \dfrac{S}{BC} ;\\\\AH= \dfrac{96}{10} =9,6$

Высота ромба равна 9,6 см.