Предмет: Геометрия,
автор: adespina2004
Даю 40 баллов!Помогите решить(с рисунком)!
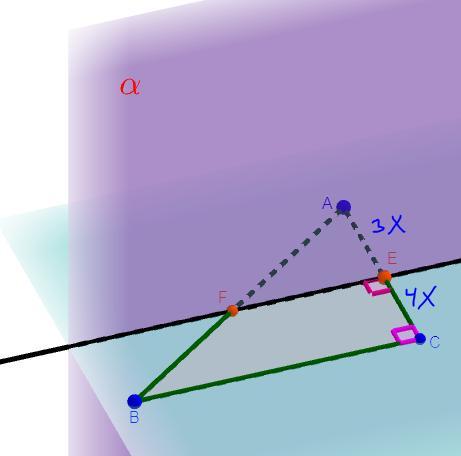
Плоскость α, перпендикулярная катету AC прямоугольного треугольника ABC, пересекает катет AC в точке E, а гипотенузу AB — в точке F.
а) Докажите, что EF ∥ BC
б) Докажите, что ∆AEF~∆ACB
в) Найдите отрезок EF, если AE : EC = 3 : 4, BC = 21 см
Ответы
Автор ответа:
3
Ответ:
EF = 9 см
Объяснение:
Дано: α ⊥ AC, α ∩ AC = E, α ∩ AB = F, BC ⊥ AC, AE : EC = 3 : 4, BC = 21 см
Доказать: EF║BC,
Найти: EF - ?
Решение: Так как по условию α ∩ AC = E, α ∩ AB = F и α ⊥ AC, то EF ⊥ AC.
По теореме EF║BC, так как BC ⊥ AC и EF ⊥ AC.
Треугольник по двум углам, так как угол ∠A - общий, а так как BC ⊥ AC и EF ⊥ AC, то ∠BCA = ∠FEA = 90°. Введем коэффициент пропорциональности x, тогда AE = 3x, CE = 4x. AC = AE + EC = 3x + 4x = 7x. По свойствам подобных треугольников (
) :
см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: aidaterzyan
Предмет: Английский язык,
автор: valera121002opel
Предмет: Физика,
автор: dimonsholpan
Предмет: Алгебра,
автор: zednar
Предмет: Биология,
автор: TynoNKaPToOIOEl