Предмет: Математика,
автор: lina3482
помогите, пожалуйста!! очень срочно нужно выполнить задания, совсем ничего не понимаю:(
Приложения:
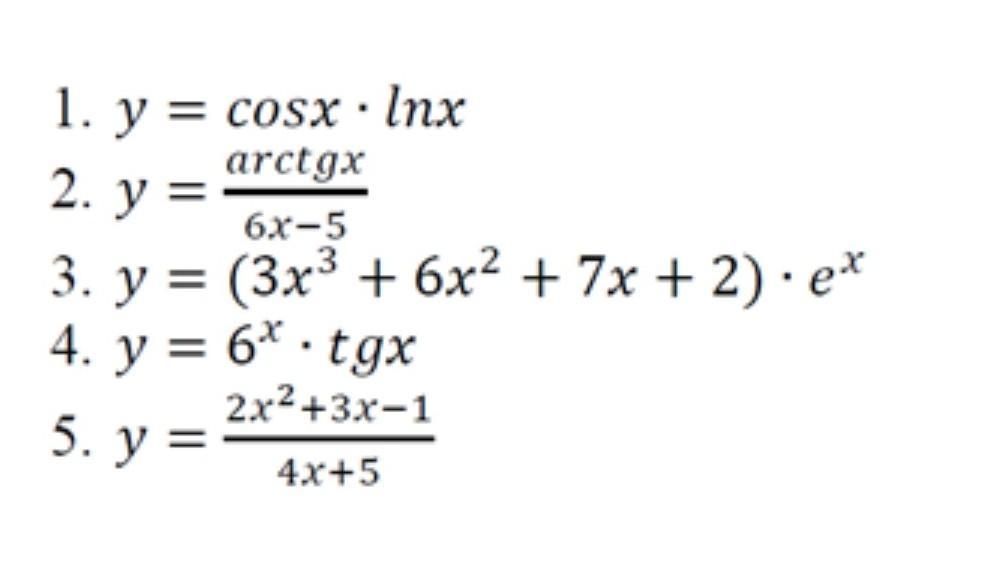
pushpull:
а сделать с этими функциями что?
найти производные функций
ок сейчас
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
здесь применяем формулы
и табличные интегралы
1) y = cosx*lnx
(cosx*lnx)' = (cosx)'*lnx+cosx*(lnx)' = -sinx*lnx+
2)
3) y=(3x³ +6x² +7x +2)eˣ
((3x³ +6x² +7x +2)eˣ)' = (3x³ +6x² +7x +2)'eˣ+(3x³ +6x² +7x +2)(eˣ)'=
= (9x²+12x+7)eˣ +(3x³ +6x² +7x +2)eˣ = (3x³ +15x² +19x +9)eˣ
4) y = 6ˣ*tgx
(6ˣ*tgx)' = (6ˣ) ' *tgx + 6ˣ *(tgx)' = 6ˣ *ln6 * tgx -
5)
Похожие вопросы
Предмет: Математика,
автор: milanamilu04
Предмет: История,
автор: darmiller2014
Предмет: Русский язык,
автор: Scalliani
Предмет: Математика,
автор: Kirigiri1
Предмет: Математика,
автор: tagievsasha686