Предмет: Математика,
автор: skhoroshilova00
Вычислить указанный предел
Приложения:
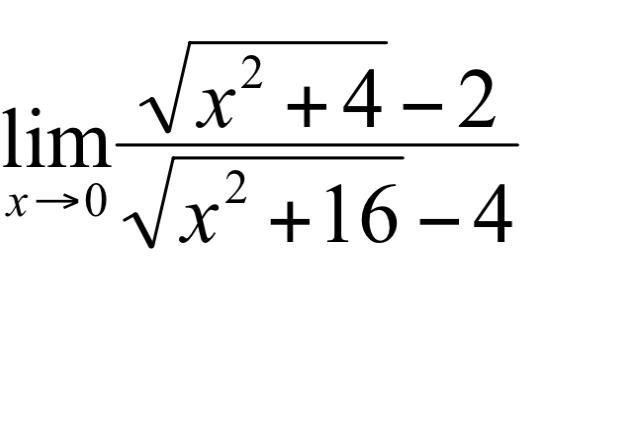
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
здесь надо избавиться от иррациональности
домножим числитель и знаменатель на соответствующие сопряженные выражения и
получим длинную дробь и потом учтем, что (a+b)(a-b) = a² - b²
и теперь можем посчитать предел
Похожие вопросы
Предмет: Биология,
автор: ЮличкаLOVE
Предмет: Алгебра,
автор: shumov1982indox
Предмет: Русский язык,
автор: shernuy
Предмет: Математика,
автор: matisseen
Предмет: Химия,
автор: dovliatova02sasha