Предмет: Математика,
автор: alpamisnurshat6
вычислите производную функций
Приложения:
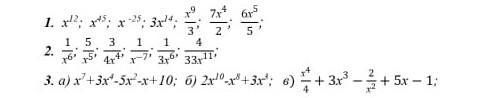
Ответы
Автор ответа:
1
Ответ:
1.
2.
3.
б)
в)
alpamisnurshat6:
Arigato!!!
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: tulucka
Предмет: Русский язык,
автор: Аноним
Предмет: История,
автор: qwertyui1123
Предмет: Биология,
автор: anyasavenkova03