Предмет: Алгебра,
автор: chellintano
найти x если ^x+75-^x=5
Приложения:
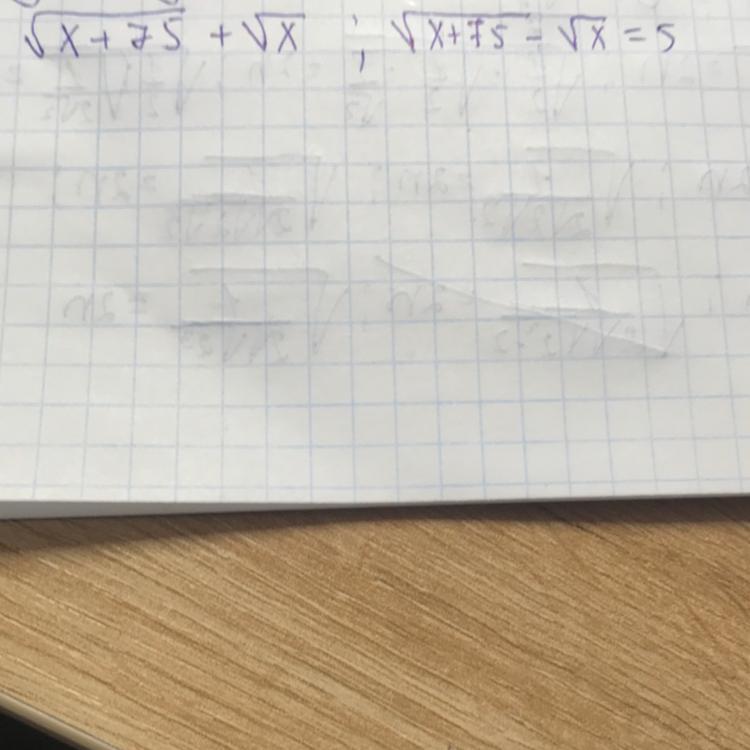
Ответы
Автор ответа:
0
Учтём, что подкоренные выражения всегда должны быть неотрицательными:
Продолжаем решать уравнение. Если получатся решения, которые не попадут в промежуток выше, то корнями они не будут.
Возведём обе части уравнения в квадрат.
Получившееся значение подпадает под область допустимых значений. Значит, уравнение имеет 1 корень.
Ответ: .
Похожие вопросы
Предмет: Математика,
автор: saageworg
Предмет: Қазақ тiлi,
автор: erkeshbaby
Предмет: Английский язык,
автор: rodrigezliza
Предмет: История,
автор: safinlinar200
Предмет: Математика,
автор: 5ангелина5