Помогите пж!Нужно сегодня!

Ответы
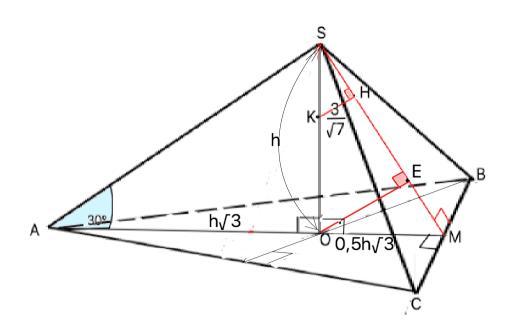
В правильной треугольной пирамиде SABC с вершиной Ѕ проведена высота ЅО. На отрезке ЅО взята точка К так, что ЅК:КО=1:3 Известно, что боковые ребра образуют с основанием углы, равные π/6, а расстояние от точки К до боковой грани составляет 3/√7. Найдите объём пирамиды.
Ответ:432 (ед. объема)
Пошаговое объяснение (подробно):
В правильной пирамиде вершина проецируется в центр основания ( для треугольной - в точку пересечения медиан).
V(SABC)=Ѕ(ABC)•SO/3.
Примем высоту ЅО=h
π/6=30°
АО=SO•сtg30°=h•√3
ОМ=AO/2=0,5h√3 (из свойства медиан).
Из отношения ЅК:КО=1:3 (дано) находим SO=4SK
Расстояние от точки (К) до плоскости (грани СSВ) равно длине проведенного к ней перпендикуляра.
Проведём ОЕ║КН перпендикулярно (SCB), т.Е принадлежит высоте SM ∆ СЅВ.
⊿ SOE~⊿ SKH
Из подобия следует ЅО:ЅК=ОЕ:КН⇒
ОЕ=4КН=12/√7
⊿ SOE~⊿ EOM
Из ⊿ ЅОМ по т.Пифагора
ЅМ²=ЅО²+ОМ²=h²+3h²/4=7h²/4⇒
SM=√(7h²/4)=h√7/2
⊿ SOM~⊿ SOE
Из подобия следует ЅО:ОЕ=ЅМ:ОМ
h:(12/√7)=(h√7/2):(h√3/2) ⇒
h=4√3 =(SO)
АМ=3•ОМ=3•0,5•(4√3)• =18
Площадь равностороннего треугольника через высоту
S(ABC)=AM²/√3=108√3
V(SABC)=[(108√3)•4√3]:3=432 (ед. объёма).