Предмет: Геометрия,
автор: Vlad001EXPERT
Решение прямоугольных треугольников. Урок 3
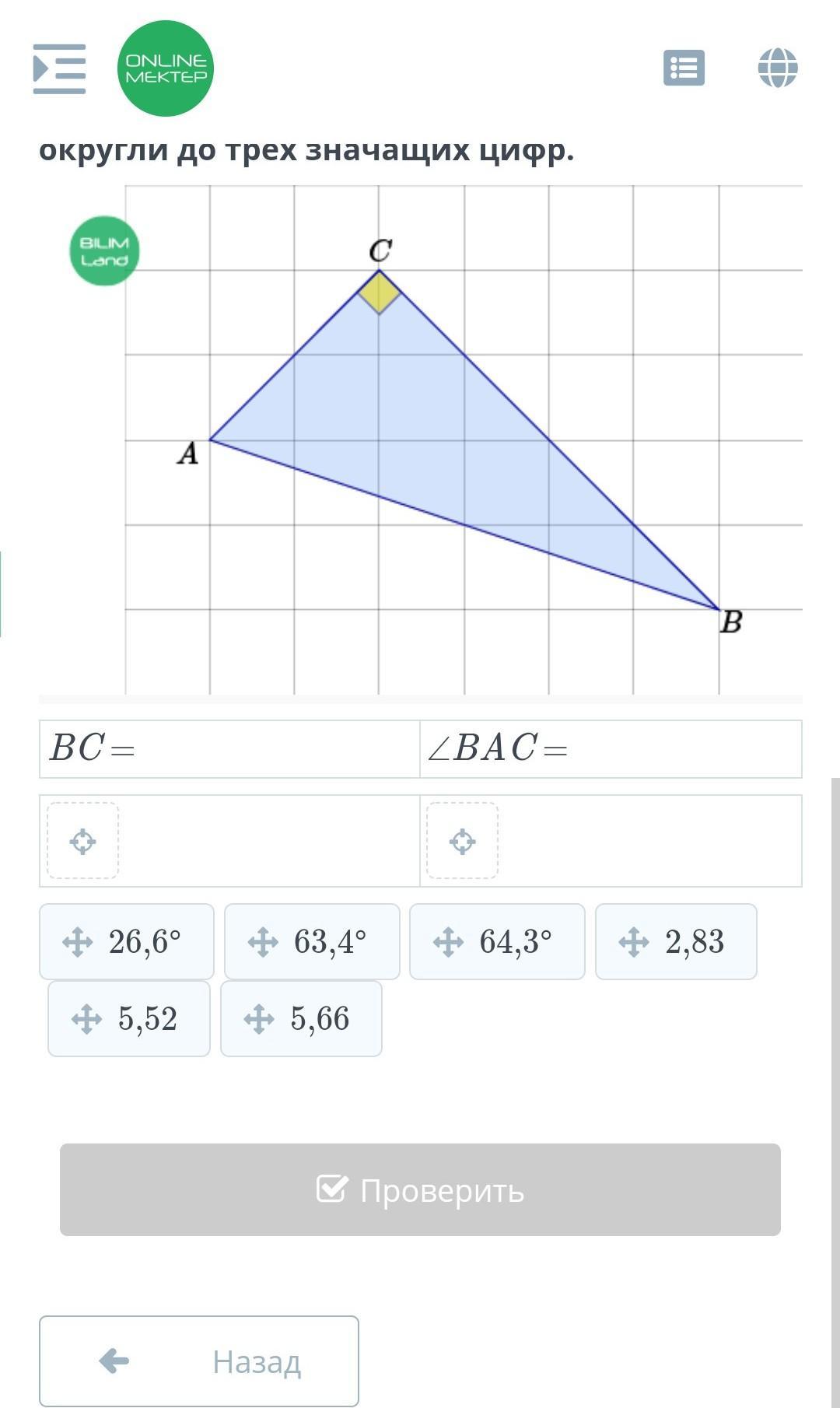
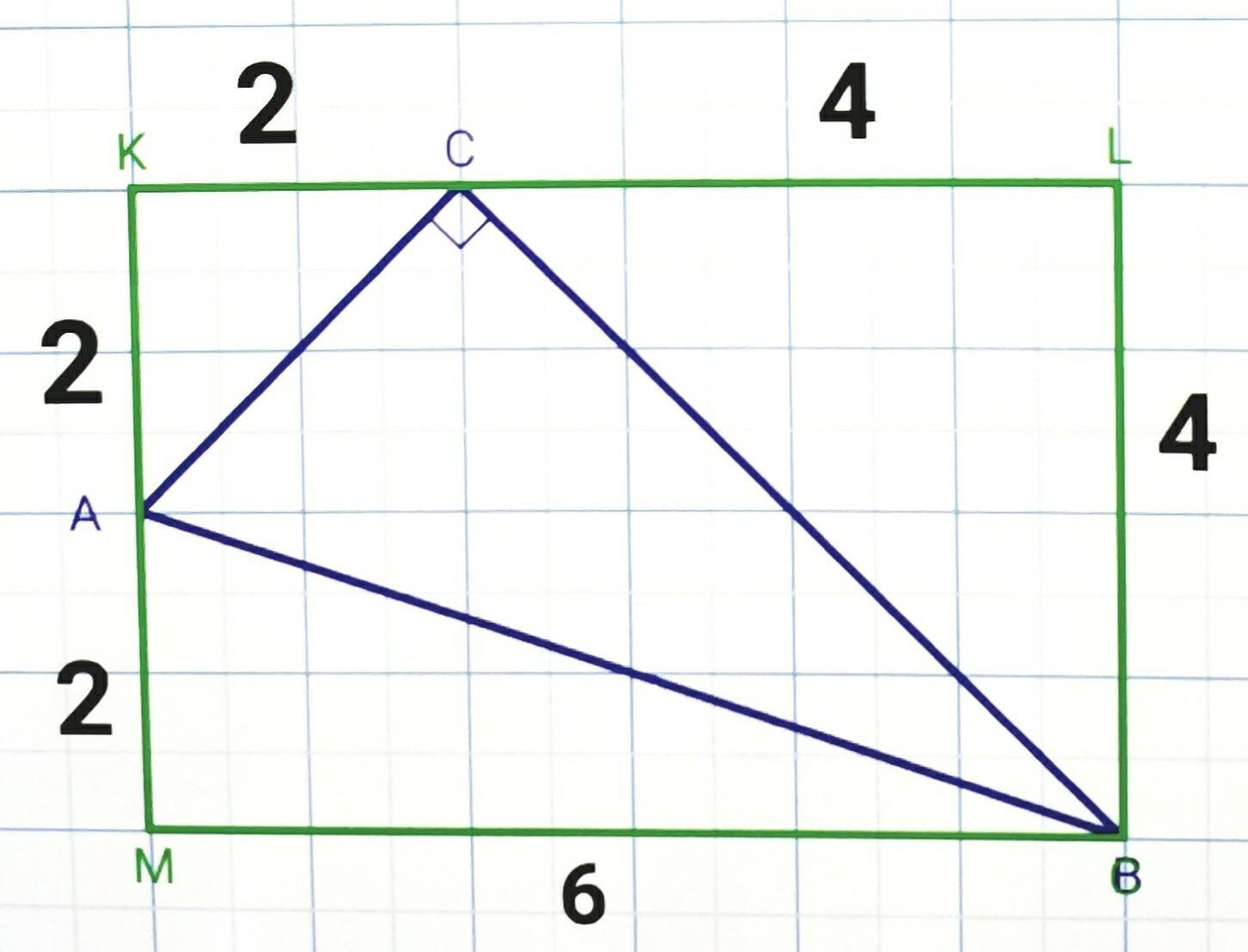
Сторона квадрата клетчатой сетки на рисунке равна 1. Найди длину наибольшего катета и величину наибольшего острого угла прямоугольного треугольника. Ответы округли до трех значащих цифр.
Приложения:
Ответы
Автор ответа:
1
Ответ:
ВС=5,66
<А=63,4°
Объяснение:
Рассмотрим прямоугольный треугольник BLC (< L=90°). По теореме Пифагора найдём гипотенузу ВС:
Рассмотрим прямоугольный треугольник АКC (<К=90°). По теореме Пифагора найдём гипотезу АC:
Наибольший острый угол лежит напротив наибольшего катета. По определению тангенса найдём угол ВАС:
Используя калькулятор находим, что угол ВАС=63,4°
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: 2093541
Предмет: Математика,
автор: GeraLowe
Предмет: Қазақ тiлi,
автор: megaievghienii
Предмет: История,
автор: АринаДаутова
Предмет: Литература,
автор: Sveta260506