Предмет: Геометрия,
автор: Аноним
ТЕКСТ ЗАДАНИЯ
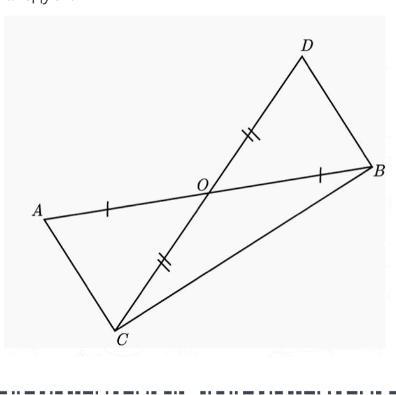
Отрезки AB и CD пересекаются в точке O, которая является серединой каждого из отрезков. OB = 7 см, BD = 4 см.
a) Чему равна длина отрезка AC?
b) Из равенства каких треугольников это следует?
Приложения:
Ответы
Автор ответа:
2
Ответ:
a) AC = 4 см
b) ΔAOC = ΔBOD
Объяснение:
Дано: AB ∩ CD = O, AO = OB, CO = DO, OB = 7 см, BD = 4 см
Найти: AC - ?
Решение: Так как по условию AB ∩ CD = O, то отрезки AB и CD образуют вертикальные углы, следовательно ∠AOC = ∠BOD. Треугольник ΔAOC = ΔBOD по первому признаку равенства треугольников, так как по условию AO = OB, CO = DO и угол ∠AOC = ∠BOD как вертикальные углы. Так как треугольник ΔAOC = ΔBOD по первому признаку равенства треугольников, то соответствующие элементы треугольников равны, следовательно AC = BD = 4 см.
Похожие вопросы
Предмет: Русский язык,
автор: Дохоян
Предмет: Математика,
автор: deflin7
Предмет: Математика,
автор: sveta2014466
Предмет: Математика,
автор: Аноним