Предмет: Математика,
автор: airanaradnaeva3012
Задание 10 класса.30 баллов
Приложения:
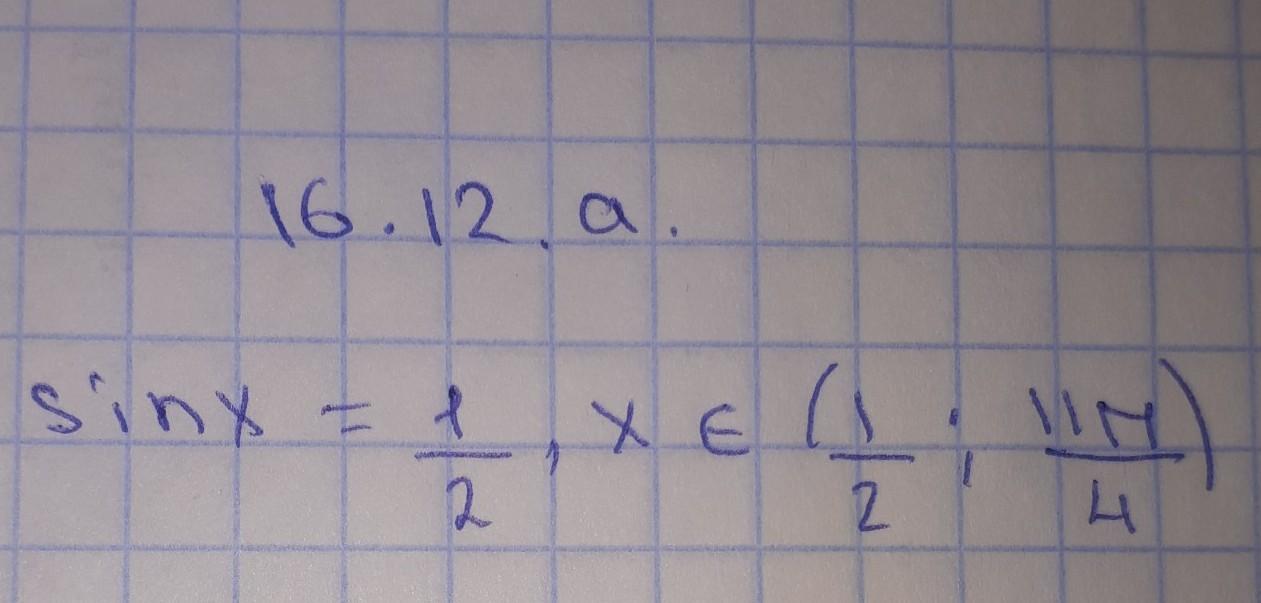
Ответы
Автор ответа:
0
Для того, чтобы определить, какие корни принадлежат заданному промежутку, достаточно решить двойное неравенство для каждой серии корней.
Так как , то
. Подставляем это значение
в первую серию корней.
Для второй серии корней делаем то же самое:
Так как , то
. Подставляем значение:
Итого мы имеем три корня уравнения, принадлежащих данному промежутку.
Ответ:
Похожие вопросы
Предмет: Физика,
автор: Аноним
Предмет: Математика,
автор: ninok149
Предмет: Литература,
автор: malythcom
Предмет: Математика,
автор: horonenkodimry